
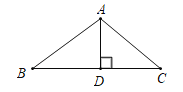
【题目】如图,已知AD是△ABC的高,且AB+BD=AC+CD,求证:AB=AC.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
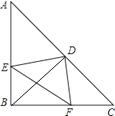
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,交AB于E,交BC于F,连接BD.
(1)求证:△CDF≌△BED
(2)若AE=4,FC=3,求AB长
查看答案和解析>>
科目:初中数学 来源: 题型:
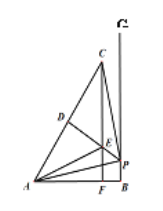
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,连接AP,作AP⊥CP且AP=CP,连接AC,PD平分∠APC,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,连接CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=mx+n与反比例函数交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1) 若m=k,n=0,求A,B两点的坐标(用m表示).
(2) 如图1,若A(x1,y1)、B(x2,y2),写出y1+y2与n的大小关系,并证明.
(3) 如图2,M、N分别为反比例函数![]() 图象上的点,AM∥BN∥x轴.若
图象上的点,AM∥BN∥x轴.若![]() ,且AM,BN之间的距离为5,则k-b=_____________
,且AM,BN之间的距离为5,则k-b=_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com