
����Ŀ��ijУҪ��С����С������ͬѧ����ѡһ�˲μ�ȫ����ѧ����������������ѡ�β����У������ijɼ��ֱ����±���

�����ϱ�����������⣺
��1������±���
���� | ����֣� | ƽ���ɼ����֣� | ��λ�����֣� | �������֣� | ���� |
�� | 40 | 80 | 75 | 75 | 190 |
�� |
��2��������β����У��ɼ��Ƚ��ȶ���ͬѧ��˭������80�����ϣ���80�֣��ijɼ���Ϊ���㣬��С����С��������β����е������ʸ��Ƕ��٣�
��3����������������ɼ��ﵽ80�����ϣ���80�֣��ͺܿ��ܻ��ɼ��ﵽ90�����ϣ���90�֣��ͺܿ��ܻ��һ�Ƚ�����ô����ΪӦѡ˭�μӱ����ȽϺ��ʣ�˵���������.
���𰸡���1������������2���ɼ��Ƚ��ȶ�����С�С����������Ϊ40%��С���������Ϊ80%����3��������.
��������
��1������ƽ��������λ�����������������ĸ��������ص�����
��2�����ӳ���ݵ���ɢ�̶������Է���ԽСԽ�ȶ���Ӧ��С��ijɼ��ȶ���С����������=![]() ��С���������=
�����������=![]() ��
��
��3��ѡ˭�μӱ����Ĵ𰸲�Ψһ��С��ijɼ��ȶ������Իļ��ʴ���С����90�����ϵijɼ�������С����һ�Ƚ��Ļ������
��1��С���ƽ����=![]() =80����λ��=80������=80������=
=80����λ��=80������=80������=![]() =40������=����������С����=90��70=20��
=40������=��������������=90��70=20��
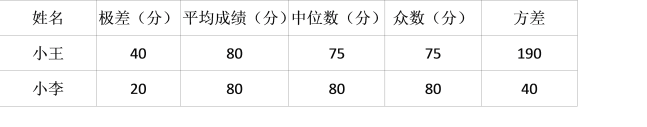
��2��������ο��������ɼ��Ƚ��ȶ�����С����С����������=![]() ��100%=40%��С���������=
��100%=40%�����������=![]() ��100%=80%��
��100%=80%��
��3������һ����ѡС��ȥ�μӱ�������ΪС��������ʸ�����4�ε�80�����ɼ��Ƚ��ȶ����������
����������ѡС��ȥ�μӱ�������ΪС���ijɼ����һ�Ƚ��Ļ��ʽϸ�����2��90�����ϣ���90�֣�������п��ܻ��һ�Ƚ���
��ע���𰸲�Ψһ����������ѡ����һ����ֻҪ�����������������֣���ѡ���˶�ȥ�μ����������ⲻ���֣���


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
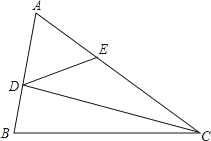
����Ŀ���ڡ�ABC�У���֪��CAB��60�㣬D��E�ֱ��DZ�AB��AC�ϵĵ㣬�ҡ�AED��60�㣬ED+DB��CE����CDB��2��CDE�����DCB����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD��EF���أ�����֪��1=��2��˵��AB//CD�����ɣ�
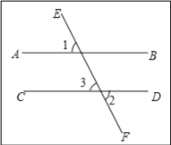
�⣺����__________ �á�2=��3������Ϊ��1=��2��
���ԡ� ________ =�� _________ ��
����____________________________ �ã�_________ // _________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ��ͬѧ˼���������⣺��ͼ1�����ǰ�һ���ı���ABCD���ı��е�E��F��G��H�������������õ����ı���EFGH��ƽ���ı�����
С����˼������ʱ��������˼·������AC��

���С����˼·������
��1����ֻ�ı�ͼ1���ı���ABCD����״����ͼ2�������ı���EFGH����ƽ���ı�����˵���������ο�С��˼���������������һ��������
��2����ͼ2���ڣ�1���������£�������AC��BD��
�ٵ�AC��BD����ʲô����ʱ���ı���EFGH�����Σ�д�����۲�֤����
�ڵ�AC��BD����ʲô����ʱ���ı���EFGH�Ǿ��Σ�ֱ��д�����ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ����ˬ���Ĺ���Բ��ͼ�������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ�ɵ�һ���������Σ���ͼ��ʾ��������������ε������25��С�����ε������1��ֱ�������ε���ֱ�DZ߷ֱ���a��b����ô![]() ��ֵΪ�� ��.
��ֵΪ�� ��.

A. 49 B. 25 C. 13 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴ٽ����ܼ��ţ�������Լ�õ磬ij�н�ʵ�о��������õ���ݵ�۷�����ͼ�����߷�ӳ��ÿ��ÿ���õ���y��Ԫ�����õ���x���ȣ���ĺ�����ϵʽ��
��1������ͼ���ݵ�۷�����Ϊ�������Σ���д�±���
���� | ��һ�� | �ڶ��� | ������ |
ÿ���õ���x���ȣ� | 0��x��140 |
��2��С����ij���õ�120�ȣ��轻��� Ԫ
��3����ڶ���ÿ�µ��y��Ԫ�����õ���x���ȣ�֮��ĺ�����ϵʽ��
��4����ÿ���õ�������230��ʱ��ÿ����1�ȵ�Ҫ�ȵڶ����ึ���mԪ��С�ռ�ij���õ�290�ȣ������153Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ����
����![]() Ϊ
Ϊ![]() ���е�.����
���е�.����![]() ��
��![]() ƽ�е�ֱ�߽�����
ƽ�е�ֱ�߽�����![]() �ڵ�
�ڵ�![]() .
.
��1����![]() ��
��![]() ��
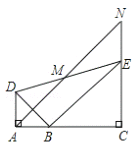
��![]() ������ͬһֱ����ʱ����ͼ1������֤��
������ͬһֱ����ʱ����ͼ1������֤��![]() Ϊ
Ϊ![]() ���е㣻
���е㣻
��2����ͼ1��![]() �Ƶ�
�Ƶ�![]() ��ת����
��ת����![]() ��
��![]() ��
��![]() ������ͬһֱ����ʱ����ͼ2������֤��
������ͬһֱ����ʱ����ͼ2������֤�� ![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
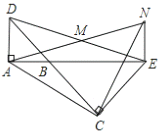
��3���ڣ�2�������£���֪![]() ��
��![]() ,��
,��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��600�����μ���Ʒ������Ϊÿ��6Ԫ����һ����ÿ��10Ԫ�ļ۸��۳�200�����ڶ�������ÿ��10Ԫ�ļ۸������Կ��۳�200�������̵�Ϊ���ʵ����������������������ۣ������г����飬����ÿ����1Ԫ���ɶ��۳�50�������ۼ۲��õ��ڽ��ۣ������۽���xԪ��������һ�ܺ��̵��ʣ�����μ���Ʒ��ִ�������ÿ��4Ԫ�ļ۸�ȫ���۳�������������μ���Ʒ������1250Ԫ���ʵڶ���ÿ�����μ���Ʒ�����ۼ۸�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺��һ�������ڽ���ȵ��ı��ν��������ڽ��ı��Ρ�.�����������⣺
(1)�����Ρ������Ρ������Ρ��С����ڽ��ı��Ρ���____________��
(2)��ͼ![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() .��֤���ı���
.��֤���ı���![]() �ǡ����ڽ��ı��Ρ���
�ǡ����ڽ��ı��Ρ���
(3)��֪���ڡ����ڽ��ı��Ρ�![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���뻭����Ӧͼ�Σ���ֱ��д��
���뻭����Ӧͼ�Σ���ֱ��д��![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com