【题目】如图，直线AB，CD被EF所截，若已知∠1=∠2，说明AB//CD的理由．
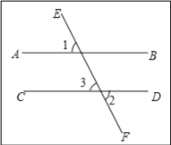
解：根据__________ 得∠2=∠3，又因为∠1=∠2，
所以∠ ________ =∠ _________ ，
根据____________________________ 得：_________ // _________ ．
科目：初中数学 来源： 题型：
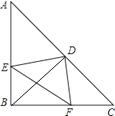
【题目】如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边中点，过D点作DE⊥DF，交AB于E，交BC于F,连接BD.
(1)求证：△CDF≌△BED
(2)若AE=4，FC=3，求AB长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)计算并观察下列各式：
第1个：(a﹣b)(a+b)＝______；
第2个：(a﹣b)(a2+ab+b2)＝______；
第3个：(a﹣b)(a3+a2b+ab2+b3)＝_______；
……
这些等式反映出多项式乘法的某种运算规律．
(2)猜想：若n为大于1的正整数，则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)＝________；
(3)利用(2)的猜想计算：2n﹣1+2n﹣2+2n﹣3+……+23+22+1＝______．
(4)拓广与应用：3n﹣1+3n﹣2+3n﹣3+……+33+32+1＝_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
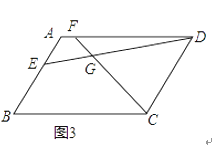
【题目】已知四边形ABCD中，EF分别是AB、AD边上的点，DE与CF交于点G．
（1）如图1，若四边形ABCD是正方形，且DE⊥CF，求证：DE=CF；
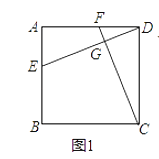
（2）如图2，若四边形ABCD是矩形，且DE⊥CF，求证：
；
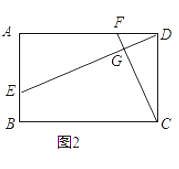
（3）如图3，若四边形ABCD是平行四边形，当∠B=∠EGF时，第（2）问的结论是否成立？若成立给予证明；若不成立，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知动点P在函数
（x＞0）的图象上运动，PM⊥x轴于点M，PN⊥y轴于点N，线段PM、PN分别与直线AB：y=﹣x+1交于点E，F，则AFBE的值为（ ）
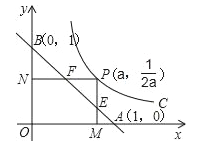
A. 4 B. 2 C. 1 D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）
A. △AFD≌△DCE B. AF=
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校要从小王和小李两名同学中挑选一人参加全国数学竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
根据上表解答下列问题：
（1）完成下表：
姓名 | 极差（分） | 平均成绩（分） | 中位数（分） | 众数（分） | 方差 |
小王 | 40 | 80 | 75 | 75 | 190 |
小李 |
（2）在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？
（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明你的理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，∠BAC=120°，点 D 是 BC 上一点，BD 的垂直平分线交 AB 于点E，将△ACD 沿 AD 折叠，点 C 恰好与点 E 重合，则∠B 等于_______°；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
