

分析 (1)首先证明四边形ADCH是平行四边形,再证明∠ADC=90°即可.
(2)与AD相等的线段有DE,AG,GC,CH,BE.构建等边三角形的判定和性质,三角形中位线定理即可判断.
解答 (1)证明:如图1中,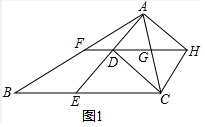
∵∠DCA=∠DCE,CD⊥AE,
∴∠CDA=∠CDE=90°,
∴∠CAD+∠DCA=90°,∠CEA+∠DCE=90°,
∴∠CAE=∠CEA,
∴AC=EC,
∴AD=DE,
∵FH∥BC,
∴AG=GC,∵DG=GH,
∴四边形ADCH是平行四边形,
∵∠ADC=90°,
∴四边形ADCH是矩形.
(2)解:如图2中,与AD相等的线段有DE,AG,GC,CH,BE.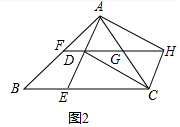
理由:∵CA=CE,∠ACE=60°,
∴△ACE是等边三角形,
∵FH∥BC,AD=DE,
∴△ADG是等边三角形,DF是△ABE的中位线,
∴与AD相等的线段有BE,DE,CG,AG,CH.
点评 本题考查矩形的判定和性质、等边三角形的判定和性质,平行线等分线段定理,三角形中位线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
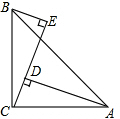 如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.
如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1、-2 | B. | -2、-1 | C. | 2、-1 | D. | -1、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星这一光明的象征联系在一起,请你画出这个对称图形的对称轴或对称中心.
如图是巴西FURNAS电力公司的标志及结构图,作者用一大一小两颗星巧妙地重叠组合,自然地把高压输电塔与五角星这一光明的象征联系在一起,请你画出这个对称图形的对称轴或对称中心.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{4}$ | B. | -$\frac{7}{11}$ | C. | $\sqrt{2}$ | D. | $\root{3}{-125}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com