练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

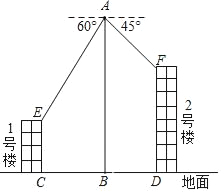
    【题目】如图，某兴趣小组用无人机进行航拍测高，无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处，测得1号楼顶部E的俯角为60°，测得2号楼顶部F的俯角为45°．已知1号楼的高度为20米，则2号楼的高度为_____米(结果保留根号)．

    【答案】(50﹣10)

    【解析】

    如图，作EG⊥AB于G，作FH⊥AB与H.在Rt△AEG中求出EG的长，再在在Rt△AFH中求出AH的长，进而可求出答案.

    如图，作EG⊥AB于G，作FH⊥AB与H.

    ∵AB=50米，CE=20米，

    ∴AG=50-20=30米，

    ∵1号楼顶部E的俯角为60°，

    ∴∠EAG=30°，

    ∵tan∠EAG=,

    ∴EG=米,

    ∵B是CD的中点，

    ∴BD=BC=EG米，

    ∴FG= BD米，

    ∵2号楼顶部F的俯角为45°，

    ∴∠HAF=45°，

    ∴AH=HF米,

    DF=BH=AB-AH=(50﹣10)米.

    故答案为：(50﹣10)米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

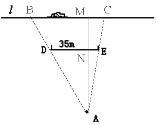
    【题目】如示意图，小华家（点A处）和公路（l）之间竖立着一块35m长且平行于公路的巨型广告牌（DE）．广告牌挡住了小华的视线，请在图中画出视点A的盲区，并将盲区内的那段公路计为BC．一辆以60km/h匀速行驶的汽车经过公路段的时间是3s，已知广告牌和公路的距离是40m，求小华家到公路的距离．（精确到1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

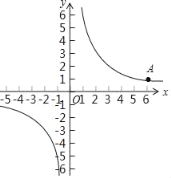
    【题目】在平面直角坐标系xOy中，反比例函数y＝的图象过点A（6，1）．

    （1）求反比例函数的表达式；

    （2）过点A的直线与反比例函数y＝图象的另一个交点为B，与y轴交于点P，若AP＝3PB，求点B的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：在平面直角坐标系xOy中，直线y＝a（x﹣m）+k称为抛物线y＝a（x﹣m）2+k的关联直线．

    （1）求抛物线y＝x2+6x﹣1的关联直线；

    （2）已知抛物线y＝ax2+bx+c与它的关联直线y＝2x+3都经过y轴上同一点，求这条抛物线的表达式；

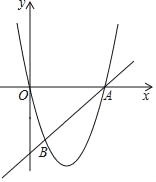
    （3）如图，顶点在第一象限的抛物线y＝﹣a（x﹣1）2+4a与它的关联直线交于点A，B（点A在点B的左侧），与x轴负半轴交于点C，连结AC、BC．当△ABC为直角三角形时，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，直线AB与抛物线y＝ax2+bx交于点A（6，0）和点B（1，﹣5）．

    （1）求这条抛物线的表达式和直线AB的表达式；

    （2）如果点C在直线AB上，且∠BOC的正切值是，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

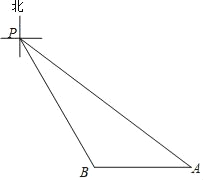
    【题目】如图，P点是某海域内的一座灯塔的位置，船A停泊在灯塔P的南偏东53°方向的50海里处，船B位于船A的正西方向且与灯塔P相距20海里．(本题参考数据sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．)

    (1)试问船B在灯塔P的什么方向？

    (2)求两船相距多少海里？(结果保留根号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    (1)x2+6x﹣2＝0(配方法)

    (2)已知关于x的方程2x2+(k﹣2)x+1＝0有两个相等的实数根，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

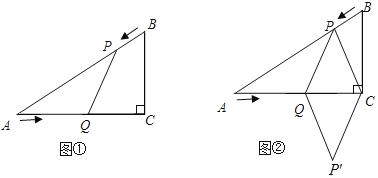
    【题目】已知：如图①，在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜4），解答下列问题：

    （1）当t为何值时，PQ∥BC；

    （2）设△AQP的面积为y（cm2），求y与t之间的函数关系式；

    （3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；

    （4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在的正方形方格中，每个小正方形的边长都为1，顶点都在网格线交点处的三角形， 是一个格点三角形．

    在图中，请判断与是否相似，并说明理由；

    在图中，以O为位似中心，再画一个格点三角形，使它与的位似比为2：1

    在图中，请画出所有满足条件的格点三角形，它与相似，且有一条公共边和一个公共角．

    查看答案和解析>>

    同步练习册答案