
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() 、y=
、y=![]() 的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
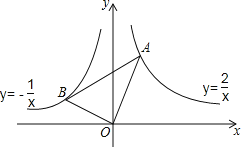
A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变
【答案】D
【解析】
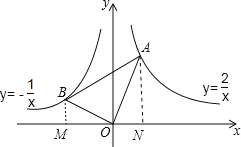
试题分析:如图,作辅助线;首先证明△BOM∽△OAN,得到![]() ;设B(﹣m,
;设B(﹣m,![]() ),A(n,
),A(n,![]() ),得到BM=
),得到BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,进而得到mn=
,OM=m,ON=n,进而得到mn=![]() ,mn=
,mn=![]() ,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=
,此为解决问题的关键性结论;运用三角函数的定义证明知tan∠OAB=![]() 为定值,即可解决问题.
为定值,即可解决问题.
解:如图,分别过点A、B作AN⊥x轴、BM⊥x轴;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴![]() ;
;
设B(﹣m,![]() ),A(n,
),A(n,![]() ),
),
则BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,
,OM=m,ON=n,
∴mn=![]() ,mn=
,mn=![]() ;
;
∵∠AOB=90°,
∴tan∠OAB=![]() ①;
①;
∵△BOM∽△OAN,
∴![]() =
=![]() =
=![]() =
=![]() ②,
②,
由①②知tan∠OAB=![]() 为定值,
为定值,
∴∠OAB的大小不变,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+m的图象和y轴交于点B,与正比例函数y=![]() x图象交于点P(2,n).
x图象交于点P(2,n).
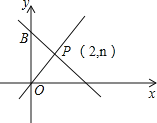
(1)求m和n的值;
(2)求△POB的面积.
考点:两条直线相交或平行问题;二元一次方程组的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年10月18日,TCL2015长沙国际马拉松赛正式开赛,来自国内外的1.5万余名选手在长沙这座美丽的城市中奔跑.马拉松长跑是国际上非常普及的长跑比赛项目,全程距离约为42千米,将数据42千米用科学记数法表示为( )
A. 42×103米 B. 0.42×105米 C. 4.2×104米 D. 4.2×105米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com