
【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;
![]()
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,﹣3)★(3,﹣2)= ;
(2)若有理数对(﹣3,2x﹣1)★(1,x+1)=7,则x= ;
(3)当满足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
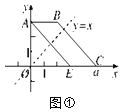
【题目】如图①,在平面直角坐标系xOy中,已知点A(0,3),B(2,3),OC=a.将梯形ABCO沿直线y=x折叠,点A落在线段OC上,对应点为E.
(1)求点E的坐标;
(2)①若BC∥AE,求a的值;(提示:两边互相平行的四边形是平行四边形,平行四边形的对边相等)
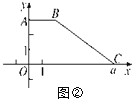
②如图②,若梯形ABCO的面积为2a,且直线y=mx将此梯形面积分为1∶2的两部分,求直线y=mx的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有七个完全相同的小球,小球上分别标有-3、-2、-1、0、1、2、3七个数,搅匀后一次从中摸出一个小球,将小球上的数用![]() 表示,将
表示,将![]() 的值分别代入函数
的值分别代入函数![]() 和方程
和方程![]() ,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的
,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的![]() 的值之和是( )
的值之和是( )
A. 1 B. -1 C. -3 D. -4
查看答案和解析>>
科目:初中数学 来源: 题型:
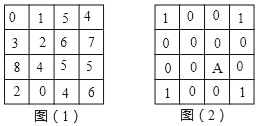
【题目】在图(1)中,对任意相邻的上下或左右两格中的数字同时加1或减2,这算作一次操作,经过若干次操作后,图(1)能变为图(2),则图(2)中A格内的数是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,∠AOB和∠COD都是直角,
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=100°,∠COD=110°,若∠AOD=∠BOC+70°,求∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC. 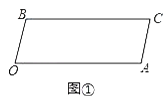
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数. 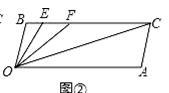
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. 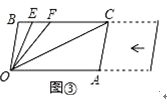
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com