
【题目】(1)如图1,∠AOB和∠COD都是直角,
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=100°,∠COD=110°,若∠AOD=∠BOC+70°,求∠AOC的度数.

【答案】(1)①30;30;②相等,理由详见解析;(2)∠AOC=30°.
【解析】
(1)①根据直角定义可得∠COD=∠AOB=90°,再利用角的和差关系可得答案;
②根据条件可得∠AOB=∠COD,再用等式的性质可得∠AOB-∠COB=∠COD-∠BOC,进而可得结论;
(2)设∠AOC=x°,则∠BOC=(100-x)°,然后再表示出∠BOD,进而可得∠AOD=∠AOB+∠BOD=100°+10°+x°=100°-x°+70°,再解方程即可.
解:(1)①∵∠COD是直角,
∴∠COD=90°,
∵∠BOC=60°,
∴∠BOD=30°,
∵∠AOB是直角,
∴∠AOB=90°,
∵∠BOC=60°,
∴∠AOC=30°,
故答案为:30;30;
②相等,
∵∠AOB和∠COD都是直角,
∴∠AOB=∠COD,
∴∠AOB﹣∠COB=∠COD﹣∠BOC,
即∠BOD=∠AOC;
(2)设∠AOC=x°,则∠BOC=(100﹣x)°,
∵∠COD=110°,
∴∠BOD=110°﹣(100﹣x)°=x°+10°,
∵∠AOD=∠BOC+70°,
∴∠AOD=∠AOB+∠BOD=100°+10°+x°=100°﹣x°+70°,
解得:x=30,
∴∠AOC=30°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据衢州市统计局发布的统计数据显示,衢州市近5年国民生产总值数据如图1所示,2016年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示。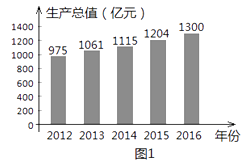
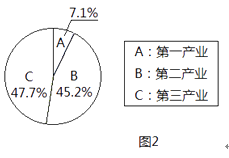
请根据图中信息,解答下列问题:
(1)求2016年第一产业生产总值(精确到1亿元);
(2)2016年比2015年的国民生产总值增加了百分之几(精确到1%)?
(3)若要使2018年的国民生产总值达到1573亿元,求2016年至2018年我市国民生产总值平均年增长率(精确到1%)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A、B、C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O时,点P、Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P、Q两点相遇?
(2)当P在线段AB上且PA=3PB时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.
(1)求长方形硬纸片的宽;
(2)小梅想用该长方形硬纸片制作一个体积512cm3的正方体的无盖笔筒,请你判断该硬纸片是否够用?若够用,求剩余的硬纸片的面积;若不够用,求缺少的硬纸片的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.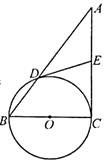
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整) 解:∠AGD=∠ACB.理由如下:
∵EF⊥AB,CD⊥AB(已知)
∴∠EFB=∠CDB=90° ()
∴∥(同位角相等,两直线平行)
∴∠1=∠ECD()
又∵∠1=∠2(已知)
∴∠ECD=( 等量代换)
∴GD∥CB()
∴∠AGD=∠ACB ().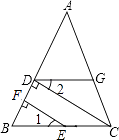
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,不正确的个数有( ) ①所有的正数都是整数②|a|一定是正数 ③无限小数一定是无理数 ④(﹣2)3没有平方根 ⑤ ![]() 的平方根是±4 ⑥
的平方根是±4 ⑥ ![]() .
.
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com