
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.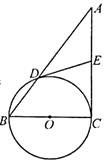
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.
【答案】
(1)
证明:连结OD,∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADE+∠BDO=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
又∵OD=OB,
∴∠B=∠BDO,
∴∠ADE=∠A.
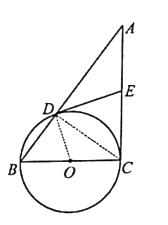
(2)
解:连结CD,∵∠ADE=∠A,
∴AE=DE,
∵BC是⊙O的直径,∠ACB=90°.
∴EC是⊙O的切线,∴DE=EC,
∴AE=EC.
又∵DE=10,
∴AC=2DE=20,
在Rt△ADC中,DC= ![]() .
.
设BD=x,
在Rt△BDC中,BC2=x2+122, 在Rt△ABC中,BC2=(x+16)2-202,
∴x2+122=(x+16)2-202,解得x=9,
∴BC= ![]() .
.

【解析】(1)连结OD,根据切线的性质和同圆的半径相等,及圆周角所对的圆周角为90°,得到相对应的角的关系,即可证明;(2)由(1)中的∠ADE=∠A可得AE=DE;由∠ACB=90°,可得EC是⊙O的切线,由切线长定理易得DE=EC,则AC=2DE,由勾股定理求出CD;设BD=x,再可由勾股定理BC2= x2+122=(x+16)2-202,可解出x的值,再重新代入原方程,即可求出BC.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:
【题目】根据下列条件画图
如图示点A、B、C分别代表三个村庄.
(1)画射线AC;
(2)画线段AB;
(3)若线段AB是连结A村和B村的一条公路,现C村庄也要修一条公路与A、B两村庄之间的公路连通,为了减少修路开支,C村庄应该如何修路?请在同一图上用三角板画出示意图,并说明画图理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有七个完全相同的小球,小球上分别标有-3、-2、-1、0、1、2、3七个数,搅匀后一次从中摸出一个小球,将小球上的数用![]() 表示,将
表示,将![]() 的值分别代入函数
的值分别代入函数![]() 和方程
和方程![]() ,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的
,恰好使得函数的图像经过二、四象限,且方程有整数解,那么这7个数中所有满足条件的![]() 的值之和是( )
的值之和是( )
A. 1 B. -1 C. -3 D. -4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,∠AOB和∠COD都是直角,
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=100°,∠COD=110°,若∠AOD=∠BOC+70°,求∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( ) 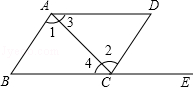
A.∠D+∠DAB=180°
B.∠B=∠DCE
C.∠1=∠2.
D.∠3=∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用![]() 纸在某誊印社复印文件,复印页数不超过
纸在某誊印社复印文件,复印页数不超过![]() 时每页收费
时每页收费![]() 元;复印页数超过
元;复印页数超过![]() 时,超过部分每页收费
时,超过部分每页收费![]() 元.在某图书馆复印同样的文件,不论复印多少页,每页收费
元.在某图书馆复印同样的文件,不论复印多少页,每页收费![]() 元,如何根据复印的页数选择复印的地点使总价格比较便宜?
元,如何根据复印的页数选择复印的地点使总价格比较便宜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B表示的数分别是有理数a,b.
(1)若点A在原点的左侧,点B在原点的右侧,且|a|=|b|,则a与b的关系是 ,用式子表示为 .
(2)若a=﹣5,b=1![]()
①分别写出a,b的相反数;
②求|a![]() |﹣|b
|﹣|b![]() |的值.
|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com