
| A. | 24 | B. | 54 | C. | 9$\sqrt{3}$ | D. | 54$\sqrt{3}$ |
分析 边长为6的正六边形可以分成六个边长为6的正三角形,计算出正六边形的面积即可.
解答 解:连接正六变形的中心O和两个顶点D、E,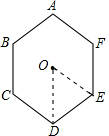
得到△ODE,
因为∠DOE=360°×$\frac{1}{6}$=60°,
又因为OD=OE,
所以∠ODE=∠OED=(180°-60°)÷2=60°,
则三角形ODE为正三角形,
∴OD=OE=DE=6,
∴S△ODE=$\frac{1}{2}$OD•OE•sin60°=$\frac{1}{2}$×6×6×$\frac{\sqrt{3}}{2}$=9$\sqrt{3}$.
正六边形的面积为6×9$\sqrt{3}$=54$\sqrt{3}$.
故选D.
点评 本题考查学生对正多边形的概念掌握和计算的能力,不仅要熟悉正六边形的性质,还要熟悉正三角形的面积公式.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
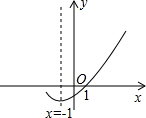 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
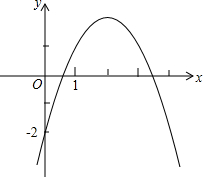 函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.
函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.| A. | 1 | B. | 2 | C. | 3 | D. | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
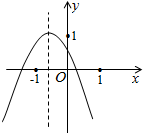 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
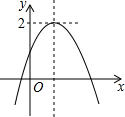 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AD=2AB
如图,矩形ABCD中,AD=2AB查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
| A. | 18,19 | B. | 18,19.5 | C. | 5,4 | D. | 5,4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com