
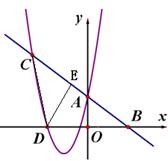
已知直线 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.
(1)当点C坐标为( ,
,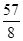 )时,求直线AB的解析式;
)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数 的图像上,求点D到直线AB的距离;
的图像上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数 有最小值-3,求实数m的值.
有最小值-3,求实数m的值.
(1) ;(2)4.8;(3)7或-7.
;(2)4.8;(3)7或-7.
解析试题分析:(1)把C点坐标分别代入二次函数解析式,求出m的值;把A(0,b)代入二次函数解析式,求出b的值,再把C点坐标代入直线解析式,求出k的值,从而可求直线解析式;
(2)由(1)知点B的坐标,从而可确定点D的坐标,然后用面积法可求点D到直线AB的距离;
(3)进行分类讨论,分别求出m的值.
试题解析:(1)∵点C( ,
,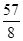 )在抛物线上,
)在抛物线上,
∴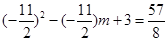
解得:m=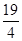 ,
,
∴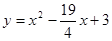
在直线 中,令x=0,则y=b,
中,令x=0,则y=b,
∴A(0,b)
把A点坐标代入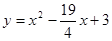 得,b=3
得,b=3
即A(0,3)
把( ,
,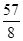 ),A(0,3)代入
),A(0,3)代入 ,得
,得 ,解得:
,解得: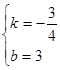 ,
,
所以直线AB的解析式为: .
.
(2)令y=0,则x=4,故B(4,0)
∴D(-4,0).
连接CD,在△BCD中,BD=8,BC=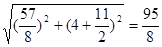
过D作DE⊥BC,垂足为E.则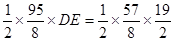 .
.
解得:DE=4.8
(3)∵抛物线的对称轴为 ,
,
∴当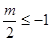 时,x=-1时二次函数的最小值为-3,得:
时,x=-1时二次函数的最小值为-3,得: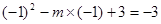 ,
,
解得:m=-7;
当-1<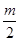 <1时,x=
<1时,x=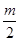 时二次函数的最小值为-3,得:
时二次函数的最小值为-3,得: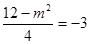 ,
,
解得:m=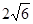 或
或 ,舍去.
,舍去.
当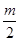 ≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
所以实数m的值为7或-7.
考点: 二次函数综合题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
(12分)如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
(1)填空:点D的坐标为 ,点E的坐标为 ;
(2)若抛物线y=aa2+ba+c(a≠0)经过A,D,E三点,求该抛物线的解析式;
(3)若正方形和抛物线均以每秒 个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动.
① 在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围;
② 运动停止时,请直接写出此时的抛物线的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数 .
.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=- x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,月利润为W外(元).
x2元的附加费,月利润为W外(元).
(1)若只在国内销售,当x=1000(件)时,y= (元/件);
(2)分别求出W内、W外与x间的函数关系式(不必写x的取值范围);
(3)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
(1)求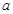 、
、 的值;
的值;
(2)求证:△OAB是等腰直角三角形;
(3)将△OAB绕点O按顺时针方向旋转l35°得到△OA′B′,写出A′B′的中点P的出标.试判断点P是否在此抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在直角梯形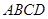 中,
中,  , 高
, 高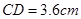 (如图1). 动点
(如图1). 动点 同时从点
同时从点 出发, 点
出发, 点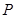 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿 运动到点
运动到点 停止,两点运动时的速度都是1cm/s,而当点
停止,两点运动时的速度都是1cm/s,而当点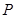 到达点
到达点 时,点
时,点 正好到达点
正好到达点 . 设
. 设 同时从点
同时从点 出发,经过的时间为
出发,经过的时间为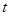 (s)时,
(s)时,  的面积为
的面积为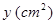 (如图2). 分别以
(如图2). 分别以 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点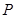 在
在 边上从
边上从 到
到 运动时,
运动时,  与
与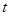 的函数图象是图3中的线段
的函数图象是图3中的线段 .
.

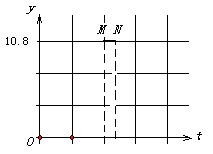
(图1) (图2) (图3)
(1)分别求出梯形中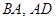 的长度;
的长度;
(2)分别写出点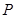 在
在 边上和
边上和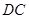 边上运动时,
边上运动时,  与
与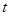 的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中 关于
关于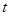 的函数关系的大致图象.
的函数关系的大致图象.
(3)问:是否存在这样的t,使PQ将梯形ABCD的面积恰好分成1:6的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣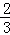 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:
(1)能否围成面积为300m2的矩形花园?若能,请写出其中一种设计方案,若不能,请说明理由.
(2)若围成一个半圆花园,则该如何设计?请写出你的设计方案.(π取3.14)
(3)围成的各种设计中,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到 ,
, ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com