
(本题10分)如图,抛物线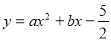 经过A(﹣1,0),B(5,0)两点.
经过A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
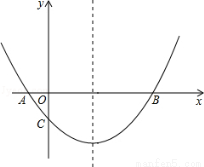
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
(1)抛物线的解析式为:y=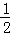 x2﹣2x﹣
x2﹣2x﹣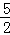 ;(2)P(2,﹣
;(2)P(2,﹣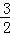 );(3)符合条件的点N的坐标为(4,﹣
);(3)符合条件的点N的坐标为(4,﹣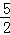 ),(2+
),(2+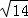 ,
,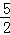 )或(2﹣
)或(2﹣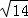 ,
,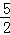 )
)
【解析】
试题分析:(1)把A(﹣1,0),B(5,0)代入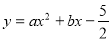 ,得
,得

解得: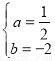
∴抛物线的解析式为:y=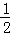 x2﹣2x﹣
x2﹣2x﹣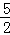 ; 3分
; 3分
(2)∵抛物线的解析式为:y= x2﹣2x﹣
x2﹣2x﹣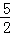 ,
,
∴其对称轴为直线x=﹣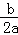 =﹣
=﹣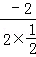 =2,
=2,
连接BC,如图1所示,
∵B(5,0),C(0,﹣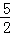 ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴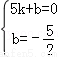 ,
,
解得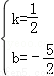 ,
,
∴直线BC的解析式为y= x﹣
x﹣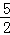 ,
,
当x=2时,y=1﹣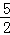 =﹣
=﹣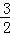 ,
,
∴P(2,﹣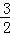 ); 3分
); 3分
(3)存在.
如图2所示,
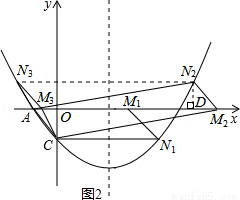
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣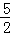 ),
),
∴N1(4,﹣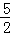 ); 2分
); 2分
②当点N在x轴上方时,
如图,过点N作ND⊥x轴于点D,
在△AND与△MCO中,
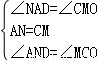
∴△AND≌△MCO(ASA),
∴ND=OC=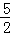 ,即N点的纵坐标为
,即N点的纵坐标为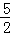 .
.
∴ x2﹣2x﹣
x2﹣2x﹣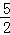 =
=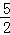 ,
,
解得x=2+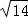 或x=2﹣
或x=2﹣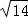 ,
,
∴N2(2+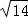 ,
,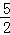 ),N3(2﹣
),N3(2﹣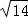 ,
,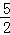 ). 2分
). 2分
综上所述,符合条件的点N的坐标为(4,﹣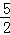 ),(2+
),(2+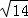 ,
,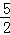 )或(2﹣
)或(2﹣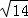 ,
,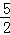 ).
).
考点:二次函数的综合运用


科目:初中数学 来源:2014-2015学年湖北省孝感市八校八年级上学期12月联考数学试卷(解析版) 题型:选择题
在直角坐标系中,已知A(3,3),在x轴、y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有( )
A.10个 B.8个 C.6个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级10月月考数学试卷(解析版) 题型:解答题
(本题8分)直线y=2x+2与x轴、y轴分别交于A、B两点,将△AOB绕点O顺时针旋转900,得到△A1OB1 。
(1)在图中画出△A1OB1;
(2)求经过A,A1,B1三点的抛物线的解析式。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:解答题
已知:如图,抛物线 与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.
与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.

(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com