
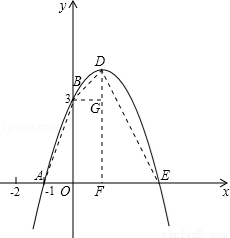
已知:如图,抛物线 与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.
与x轴、y轴分别相交于点A(﹣1,0)、B(0,3)两点,其顶点为D.

(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(1)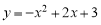 ;(2)9;(3)相似,理由见试题解析.
;(2)9;(3)相似,理由见试题解析.
【解析】
试题分析:(1)由于抛物线的解析式中只有两个未知数,因此可根据A,B两点的坐标,用待定系数法求出抛物线的解析式.
(2)由于四边形ABDE不是规则的四边形,因此可将ABDE分割成几个规则的图形后再进行求解.可设抛物线的对称轴与x轴的交点为F,那么四边形ABDE的面积=三角形AOB的面积+直角梯形BOFD的面积+三角形DFE的面积,根据抛物线的解析式可求得D、E两点的坐标,因此就可求出DF、OF、EF的长,根据A、B两点的坐标可得出OA、OB的长,那么求这些图形面积的相关线段的长就都已求出,从而可得出四边形ABDE的面积.
(3)可先根据B、D、E的坐标,求出BD、DE、BE的长,由于三角形AOB是直角三角形,要想判定两三角形是否相似,就要先判断三角形BDE是否为直角三角形,可根据BD、DE、BE三边的长以及勾股定理,来判断出三角形BDE是否为直角三角形,如果是直角三角形,那么找出三角形BDE中的直角,然后看夹直角的两组对应边是否成比例即可得出两三角形是否相似.
试题解析:(1)由已知得: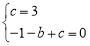 ,解得c=3,b=2,∴抛物线的线的解析式为
,解得c=3,b=2,∴抛物线的线的解析式为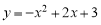 ;
;
(2)由顶点坐标公式得顶点坐标为(1,4),所以对称轴为x=1,A,E关于x=1对称,所以E(3,0),
设对称轴与x轴的交点为F,所以四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE=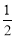 AO·BO+
AO·BO+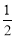 (BO+DF)·OF+
(BO+DF)·OF+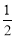 EF·DF=
EF·DF=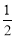 ×1×3+
×1×3+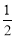 (3+4)×1+
(3+4)×1+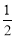 ×2×4=9;
×2×4=9;
(3)相似.如图,连接AB、BD、DE,过点D作DF⊥x轴于点F,过点B作BG⊥DF于点G.
BD=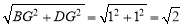 ,BE=
,BE=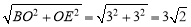 ,
,
DE=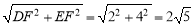 ,所以
,所以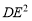 =20,即:
=20,即: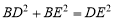 ,
,
所以△BDE是直角三角形,所以∠AOB=∠DBE=90°,且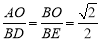 ,所以△AOB∽△DEB.
,所以△AOB∽△DEB.
考点:二次函数综合题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:2014-2015学年浙江省九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)如图,抛物线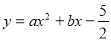 经过A(﹣1,0),B(5,0)两点.
经过A(﹣1,0),B(5,0)两点.
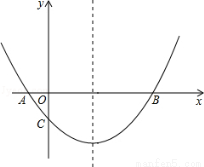
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级10月月考数学试卷(解析版) 题型:选择题
函数y=x2-3x+4的图象与坐标轴的交点个数是 ( )。
A.0 个 B.1 个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省景洪市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
下列图形中,旋转600后可以和原图形重合的是( )
A、正六边形 B、正五边形 C、正方形 D、正三角形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.

(1)求证:△ABE≌△DFE;
(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:填空题
已知一个二次函数具有性质(1)图象不经过三、四象限;(2)点(2,1)在函数的图象上;(3)当x>0时,函数值y随自变量x的增大而增大.试写出一个满足以上性质的二次函数解析式: .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:选择题
将260 000用科学记数法表示应为( )
A.0.2×106 B.26×104 C.2.6×106 D.2.6×105
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省日照市莒县北五校九年级上学期12月联考数学试卷(解析版) 题型:选择题
如图,点C为⊙O的直径AB上一动点,AB=2,过点C作DE⊥AB交⊙O于点D、E,连结AD,AE.当点C在AB上运动时,设AC的长为x,△ADE的面积为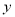 ,下列图象中,能表示
,下列图象中,能表示 与
与 的函数关系的图象大致是( )
的函数关系的图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com