
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+c��ͼ����x�ύ��A����3��0����B��2��0�����㣬��y�ύ�ڵ�C��0��3����
��1���������ߵĽ���ʽ��
��2����E��m��2����ֱ��AC�Ϸ�����������һ�㣬����EA��EB��EC��EB��y�ύ��D��
�ٵ�F��x����һ���㣬����EF������A��E��FΪ��������������BOD����ʱ������߶�EF�ij���
�ڵ�GΪy�������������һ�㣬����G��ֱ��CE�Ĵ��ߣ�����ΪH������GCH����EBA����ֱ��д����H�����꣮

���𰸡���1��y����![]() x+3����2����EF�ij�Ϊ2
x+3����2����EF�ij�Ϊ2![]() ��2���ڵ�H������Ϊ����
��2���ڵ�H������Ϊ����![]() ��
��![]() ����
����![]() ����
����
��������
��1���ô���ϵ���������������ʽ���ɣ�
��2���ٵó�![]() ����ʱ����ʱ��������ij���
����ʱ����ʱ��������ij���
�ڣ��������ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ���ó�
���ó�![]() ����
����![]() ���ó�
���ó�![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ����ã�
����ã�![]() �������
�������![]() ������ꣻ
������ꣻ
����������![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��֤��
��֤��![]() ���ɣ�����֪��
���ɣ�����֪��![]() ����
����![]() ����
����![]() ����
����![]() ��֤��
��֤��![]() ����
����![]() ��
��![]() ����
����![]() ���ó�
���ó�![]() ������
������![]() ����
����![]() �������
�������![]() �����꣮
�����꣮
�⣺��1����A����3��0����B��2��0����C��0��3������y��ax2+bx+c�ã�
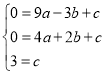 ��
��
��ã�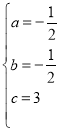 ��
��
�������ߵĽ���ʽΪ��y����![]() x+3��
x+3��
��2���ٽ�E��m��2������y����![]() x+3�У�
x+3�У�
�é�![]() m+3��0�����m����2��1����ȥ����
m+3��0�����m����2��1����ȥ����
��E����2��2����
��A����3��0����B��2��0����
��AB��5��AE��![]() ��BE��2
��BE��2![]() ��
��
��AB2��AE2+BE2��
���AEB����DOB��90����
���EAB+��EBA����ODB+��EBA��90����
���EAB����ODB��
����������FEA�ס�BODʱ��
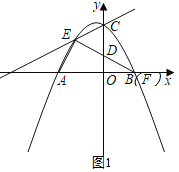
���AEF����DOB��90����
��F��B���غϣ�
��EF��BE��2![]() ��
��
����������EFA�ס�BODʱ��
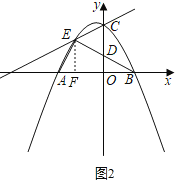
���AFE����DOB��90����
��E����2��2����
��EF��2��
�ʣ�EF�ij�Ϊ2![]() ��2��
��2��
�ڵ�![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����������H��HN��CO�ڵ�N������G��GM��HN�ڵ�M��
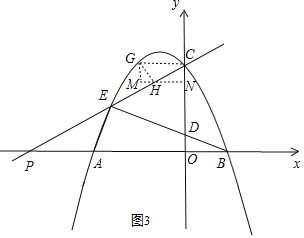
���GMN����CNH��90����
�֡�GHC��90����
���CHN+��GHM����MGH+��GHM��90����
���CHN����MGH��
��HN��CO����COP��90����
��HN��AB��
���CHN����APE����MGH��
��E����2��2����C��0��3����
��ֱ��CE�Ľ���ʽΪy��![]() x+3��
x+3��
��P����6��0����
��EP��EB��2![]() ��
��
���APE����EBA��
�ߡ�GCH����EBA��
���GCH����APE����EBA����CHN����MGH��
��GC��PB��
��C��0��3����
��G���������Ϊ3������y����![]() x+3�У��ã�x����1��0����ȥ����
x+3�У��ã�x����1��0����ȥ����
��MN��1��
�ߡ�AEB��90����AE��![]() ��BE��2
��BE��2![]() ��
��
��tan��EBA��tan��CHN��tan��MGH��![]() ��
��
��CN��MG��m����HN��2m��MH��![]() m��
m��
��MH+HN��2m+![]() m��1��
m��1��
��ã�m��![]() ��
��
��H��ęM����Ϊ��![]() ������y��
������y��![]() x+3���ã�y��
x+3���ã�y��![]() ��
��
���H����������![]() ��
��![]() ����
����
����������H��MN��PB������C��CN��MH�ڵ�N������G��GM��HM�ڵ�M��
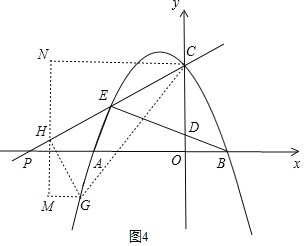
��CN��PB��
���NCH����APE��
�ɣ�����֪����APE����EBA�����NCH����EBA��
�ߡ�GMN����CNH��90����
�֡�GHC��90����
���HCN+��NHC����MHG+��NHC��90����
���HCN����MHG��
�ߡ�GCH����EBA��
���GCH����EBA����HCN����MHG��
�ɣ�����֪��![]() ����
����![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�ɣ�����֪��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��![]() ����
����![]() ��
��
![]() ������
������![]() �У��ã�
�У��ã�![]() ��0����ȥ����
��0����ȥ����
![]() ��
��
![]() ��ęM����Ϊ
��ęM����Ϊ![]() ������
������![]() ���ã�
���ã�![]() ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
�ۺ����Ͽɵõ�![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¹ڷ������鱬�����������ֳ�Ϊ������Ϊ���еķ������ʣ�������ؼ�ʱ�̣��ҹ�ij��ҵ������������ת�����֣��ⱳ�����ֳ���ҵǿ�ҵ�������θУ������ҹ������Ž�һ�Ŀ�������ľ��ģ���Ϥ����ҵ3�·ݵĿ����ղ����Ѵﵽ500��ֻ��Ԥ�ƽ�������ڶ�������ͬ���IJ��ܣ���3�·ݣ���31����㣩����ҵ�����Ŀ����������ÿ�ѧ��������ʾΪ�� ��
A.![]() ֻB.
ֻB.![]() ֻC.
ֻC.![]() ֻD.
ֻD.![]() ֻ
ֻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������IJ����У�װ�к졢�ơ�������ֻ����ɫ��ͬ��С�����к�ɫС����6�����ơ���ɫС���������ͬ��Ϊ���ƴ��л�ɫС���������ÿ�ν�����С����Ⱥ�����һ��С�������ɫ�Żأ��ٽ��ȶ�����鷢��������ɫ��Ƶ����![]() ������ƻ�ɫС��ĸ����ǣ�������
������ƻ�ɫС��ĸ����ǣ�������
A.21B.40C.42D.48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵����ۼס�������Ʒ�Ƶ�A4��ܰ칫��ֽ������2����Ʒ�ƺ�3����Ʒ�Ƶ�A4��ܰ칫��ֽ����156Ԫ������3����Ʒ�ƺ�1����Ʒ�Ƶ�A4��ܰ칫�ù���122Ԫ��
��1����������Ʒ�Ƶ�A4��ܰ칫��ֽÿ���ĵ��ۣ�
��2�������ڼ䣬Ϊ����ʦ������ֽҪ���̵��������A4��ܰ칫��ֽչ���˴����������취���£���Ʒ�Ƶ�A4��ܰ칫��ֽ��ԭ�۵İ������ۣ���Ʒ�Ƶ�A4��ܰ칫��ֽ����5���IJ��ְ�ԭ�۵��������ۣ��蹺���x����Ʒ�Ƶ�A4��ܰ칫��ֽ��Ҫy1Ԫ������x����Ʒ�Ƶ�A4��ܰ칫��ֽ��Ҫy2Ԫ���ֱ����y1��y2����x�ĺ�����ϵʽ��
��3������Ҫ����50��A4��ܰ칫��ֽʱ��������Ʒ�Ƶ�A4��ܰ칫��ֽ�����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D����ABC��BC����һ�㣬����AD������ABD�����Բ������ADC��ֱ��AD�۵�����C�Ķ�Ӧ��E���ڡ�O�ϣ�
��1����֤��AE��AB��
��2����գ�
�ٵ���CAB��90����cos��ADB��![]() ��BE��2ʱ����BC�ij�Ϊ�� ����
��BE��2ʱ����BC�ij�Ϊ�� ����
�ڵ���BAE���� ��ʱ���ı���AOED�����Σ�
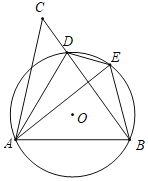
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƶ����С��Թ�ũ���о���ƶ��������ũ��һ���л���̬ˮ���ؿ����г�����ȥ����ȣ���������ˮ���IJ���������1000ǧ�ˣ�ÿǧ�˵�ƽ�������۱�ȥ�꽵����1Ԫ�����������ܶ��ȥ��������![]() ��
��
��1����֪ȥ������ˮ�����������ܶ�Ϊ10��Ԫ��������ˮ������ÿǧ�˵�ƽ���������Ƕ���Ԫ��
��2��ijˮ����ӹ�ũ��ֱ��������רӪ����ˮ�������鷢�֣���ÿǧ�˵�ƽ�����ۼ�Ϊ41Ԫ����ÿ����۳�300ǧ�ˣ���ÿǧ�˵�ƽ�����ۼ�ÿ����3Ԫ��ÿ��ɶ�����180ǧ�ˣ���ˮ����һ�������Ϊ![]() Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
Ԫ����ÿǧ�˵�ƽ�����ۼ�Ϊ����Ԫʱ����ˮ����һ������������������Ƕ��٣����������ʱ���������ú��Բ��ƣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪A��B���������ֱ�Ϊ��2![]() ��0������0��10����P�ǡ�AOB���Բ��C�ϵ�һ�㣬OP��AB�ڵ� D��
��0������0��10����P�ǡ�AOB���Բ��C�ϵ�һ�㣬OP��AB�ڵ� D��
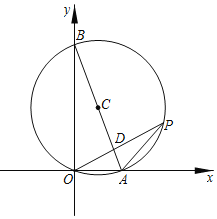
��1����OP��ABʱ����OP��
��2������AOP��30��ʱ����AP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽԺʿ̸����������״��������ʱ˵����������Ҫ���ӷ�������Ҳ���ؿֻţ�������ȥ��Ա�ܼ��ij��������Ŵ����֣�������ע��ͨ�磬��ϴ�֣����˶����ٰ�ҹ����ij����Ϊ�˼�ǿ�������������״����������֪ʶ���˽⣬ͨ����Ⱥ��������״�������ķ���֪ʶ�������������������߲�������2020������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�����������Ա����Ӽס�������С������ȡ20����Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�����ͳ�ơ��������������£�
�ռ�����
������85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
������80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
��������
�ɼ�x���֣� | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
���� | 2 | 5 | a | b |
���� | 3 | 7 | 5 | 5 |
��������
ͳ���� | ƽ���� | ��λ�� | ���� |
���� | 85.75 | 87.5 | c |
���� | 83.5 | d | 80 |
Ӧ������
��1����գ�a���� ����b���� ����c���� ����d���� ����
��2������С������800�˲�����������Ƽ�С���ɼ�����90�ֵ�������
��3����������Ա����ͳ�����ݣ���Ϊ��С��������״����������֪ʶ���ո��ã�����д����������Ա�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ο���ѧϰ�л��,��ʦ���������һ������:
��P��������ABCD�ڵ�һ��,����P��ֱ��l�ֱ������ε������ڵ�M��N,ʹ��P���߶�MN�����ȷֵ�,������ֱ���ܹ�������?
����˼��,��ͬѧ�������»���:
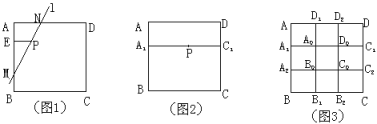
��ͼ1,����P��PE��AB��E,��EB��ȡ��M,ʹEM=2EA,��ֱ��MP��AD��N,��ֱ��MN���Ƿ���������ֱ��l.
����������Ϣ,�����������:
(1)��ͬѧ�Ļ����Ƿ���ȷ?��˵������.
(2)��ͼ1��,�ܷ�������Ŀ������ֱ��?�����,��ֱ����ͼ1�л���.
(3)��ͼ2,A1��C1�ֱ���������ABCD�ı�AB��CD�ϵ����ȷֵ�,��A1C1��AD.����P���߶�A1C1��ʱ,�ܷ�������Ŀ������ֱ��?�����,���Ի�������?
(4)��ͼ3,������ABCD�߽��ϵ�A1��A2��B1��B2��C1��C2��D1��D2�������ڱߵ����ȷֵ�.����P��������ABCD�ڵIJ�ͬλ��ʱ,������,������Ŀ������ֱ��l�����������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com