
【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。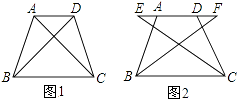
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
【答案】
(1)证明:在△ABC和△DCB中,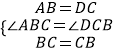
∴△ABC≌△DCB(SAS)
∴AC=DB
(2)解:BF=CE,理由如下:根据题意得:AE=DF,
∴AF=DE,
∵AD∥BC,
∴∠BAD+∠ABC=180°,∠CDA+∠DCB=180°,
∵∠ABC=∠DCB,
∴∠BAD=∠CDA,
在△BAF和△CDE中,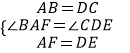
∴△BAF≌△CDE(SAS),
∴BF=CE.
【解析】(1)根据全等三角形的判定方法SAS,得到三角形全等,得到对应边相等;(2)由已知条件和角的和差再由SAS,得到△BAF≌△CDE,得到对应边相等.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A. (-2,0) B. (0,-2) C. (1,0) D. (0,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD , AE=CF , 则下列条件中不一定能使△ABE≌△CDF的是( ) 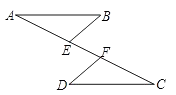
A.AB=CD
B.BE∥DF
C.∠B=∠D
D.BE=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的横断面示意图如右图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度 ![]() 和放水时间
和放水时间 ![]() 之间的关系的是( )
之间的关系的是( )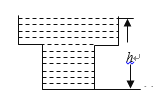
A.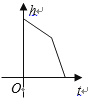
B.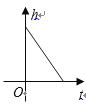
C.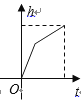
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,抛物线![]() 经过点A(0,-3),B(4,5).
经过点A(0,-3),B(4,5).
(1)求此抛物线表达式及顶点M的坐标;
(2)设点M关于y轴的对称点是N,此抛物线在A,B两点之间的部分记为图象W(包含A,B两点),经过点N的直线l: ![]() 与图象W恰一个有公共点,结合图象,求m的取值范围.
与图象W恰一个有公共点,结合图象,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com