
 (2013•大丰市一模)如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD=
(2013•大丰市一模)如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD=| 3 | 2 |
| HD |
| CD |
| EF |
| CE |
| 1 |
| 2 |
| 1 |
| 2 |
 解:(1)∵在Rt△CDE中,CD=
解:(1)∵在Rt△CDE中,CD=| 3 |
| 2 |
| CD2+DE2 |
(
|
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| CF |
| EF |
| OC |
| AE |
| t | ||
|
| DG |
| EG |
| OD |
| AE |
t+
| ||
|
| EF+CF |
| CF |
| ||
| t |
| EG+DG |
| EG |
t+
| ||||
|
| ||
| 2 |
| HD |
| CD |
| EF |
| CE |
| EF |
| CE |
| 3 |
| 5 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
| 5 |
| 2 |
| 3 |
| 20 |
| 5 |
| 2 |
| 5 |
| 2 |
 (3)①由(2)知CF=t,
(3)①由(2)知CF=t,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 18 |
| 5 |
| 18 |
| 5 |


科目:初中数学 来源: 题型:
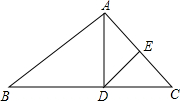 (2013•大丰市一模)如图,△ABC的周长为15cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D、交AC边于点E,连接AD,若AE=2cm,则△ABD的周长是( )
(2013•大丰市一模)如图,△ABC的周长为15cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D、交AC边于点E,连接AD,若AE=2cm,则△ABD的周长是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•大丰市一模)如图,甲、乙两名同学分别站在C、D的位置时,乙的影子与甲的影子的末端恰好在同一点,已知甲、乙两同学相距1m,甲身高1.8m,乙身高1.5m,则甲的影子是
(2013•大丰市一模)如图,甲、乙两名同学分别站在C、D的位置时,乙的影子与甲的影子的末端恰好在同一点,已知甲、乙两同学相距1m,甲身高1.8m,乙身高1.5m,则甲的影子是查看答案和解析>>
科目:初中数学 来源: 题型:
| 到康平社区供水点的路程(千米) | 运费(元/吨•千米) | |
| 甲厂 | 20 | 4 |
| 乙厂 | 14 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com