
����Ŀ���������P�ƶ���M��ת180�������Q�غϣ���ô�Ƶ�P���Q���ڵ�M�Գƣ�����M�����Գ����ģ���ʱ����M���߶�PQ���е㣮��ͼ����ֱ������ϵ�У���ABO�Ķ���A��B��O������ֱ�Ϊ��1��0������0��1������0��0��������P1��P2��P3�����е��������㶼������ABO��һ������Գƣ���P1���P2���ڵ�A�Գƣ���P2���P3���ڵ�B�Գƣ���P3���P4���ڵ�O�Գƣ���P4���P5���ڵ�A�Գƣ���P5���P6���ڵ�B�Գƣ���P6���P7���ڵ�O�Գƣ���������Щ�Գ���������ѭ������֪P1�������ǣ�1��1������P2019������Ϊ_____��
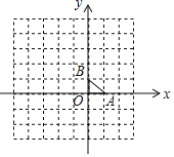
���𰸡�(-1,3)
��������
�����öԳ����ĵĶ���ֱ�ȷ��P1��P2��P3��P4��P5��P6��P7�����꣬���ֵ�P7������͵�P1��������ͬ������Щ���������6��Ϊһ�����ѭ�����ɴ˿�ȷ����P2019�����꣮
��ͼ�ߵ�P1�������ǣ�1��1����A��1��0����
����P1���P2���ڵ�A�Գƣ�
���P2��������1��1����
ͬ���õ���P3������Ϊ��1��3����
��P4��������1��3����
��P5��������1��3����
��P6��������1��1����
��P7��������1��1������
���P7������͵�P1��������ͬ��
��2019��336��6��3��
���P2019������͵�P3��������ͬ����Ϊ��1��3����
�ʴ��ǣ���1��3��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D��DF��AC������Ϊ��F��
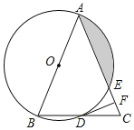
��1����֤��DFΪ��O�����ߣ�
��2����֤��FΪCE���е㣻
��3������O�İ뾶Ϊ3����CDF��22.5��������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���MΪax2+bx+c��0��NΪcx2+bx+a��0��a��c���������н��ۣ������5�Ƿ���M��һ��������ô![]() �Ƿ���N��һ���������������M����������ȵ�ʵ��������ô����NҲ����������ȵ�ʵ���������������M�뷽��N��һ����ͬ�ĸ�����ô���������x��1��������ȷ�Ľ����ǣ�������
�Ƿ���N��һ���������������M����������ȵ�ʵ��������ô����NҲ����������ȵ�ʵ���������������M�뷽��N��һ����ͬ�ĸ�����ô���������x��1��������ȷ�Ľ����ǣ�������
A.�٢�B.�٢�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��x2��4x+3��
��1�����䷽����y��x2��4x+3����y��a��x��h��2+k����ʽ��
��2����ƽ��ֱ������ϵ�У�����������κ�����ͼ��
��3��д����xΪ��ֵʱ��y��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
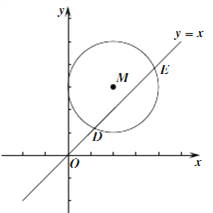
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
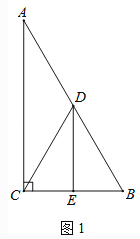
����Ŀ����Rt��ABC�У���ACB=90������A=30������D��AB���е㣬DE��BC������Ϊ��E������CD��
��1����ͼ1��DE��BC��������ϵ���� ����
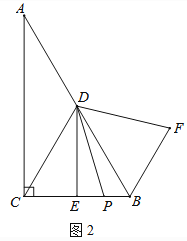
��2����ͼ2����P���߶�CB��һ���㣨��P�����B��C�غϣ�������DP�����߶�DP�Ƶ�D��ʱ����ת60�����õ��߶�DF������BF�������DE��BF��BP����֮���������ϵ����֤����Ľ��ۣ�
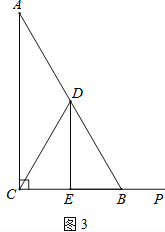
��3������P���߶�CB�ӳ�����һ���㣬���գ�2���е�����������ͼ3�в�ȫͼ�Σ���ֱ��д��DE��BF��BP����֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��˫����
��˫����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
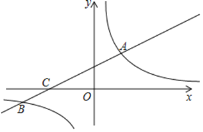
��1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() ��
��![]() ���ϣ���
���ϣ���![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
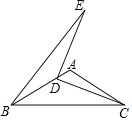
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����BAC��120������DΪAB����һ�㣨�����B�غϣ�������CD�����߶�CD�Ƶ�D��ʱ����ת90������C�Ķ�Ӧ��ΪE������BE����AB��2�����BDE��������ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ĺ���y=ax2+(2a+1)x+a-1�����������������㣬��a��ȡֵ�У� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com