
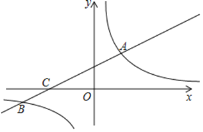
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)y=![]() x+2;(2)点P的坐标为(﹣6,0)或(﹣2,0).
x+2;(2)点P的坐标为(﹣6,0)或(﹣2,0).
【解析】
(1)求直线的解析式,就是求其中k,b的值,待定系数法即可,但需要找到两个点,发现A,B两个点在直线上,只需要知道A,B两点的坐标即可,因为A,B同时在双曲线上,代入双曲线方程即可求出A,B的坐标,进而可求出直线的解析式;
(2)因为P点在![]() 轴上,可以把P的坐标设为
轴上,可以把P的坐标设为![]() ,利用两个三角形面积之间的关系,找到关于
,利用两个三角形面积之间的关系,找到关于![]() 的方程即可求出x的值.
的方程即可求出x的值.
解:(1)∵点A(m,3),B(﹣6,n)在双曲线y=![]() 上,
上,
∴m=2,n=﹣1,
∴A(2,3),B(﹣6,﹣1).
将(2,3),B(﹣6,﹣1)代入y=kx+b,
得![]()
解得![]() .
.
∴直线的解析式为y=![]() x+2.
x+2.
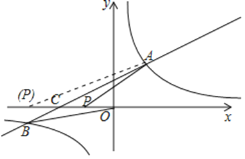
(2)当y=![]() x+2=0时,x=﹣4,
x+2=0时,x=﹣4,
∴点C(﹣4,0).
设点P的坐标为(x,0),
∵S△ACP=![]() S△BOC,A(2,3),B(﹣6,﹣1),
S△BOC,A(2,3),B(﹣6,﹣1),
∴![]() ×3×|x﹣(﹣4)|=
×3×|x﹣(﹣4)|=![]() ×
×![]() ×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
解得:x1=﹣6,x2=﹣2.
∴点P的坐标为(﹣6,0)或(﹣2,0).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是【 】
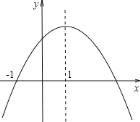
(A) ①② (B) ②③ (C) ③④ (D)①④
查看答案和解析>>
科目:初中数学 来源: 题型:
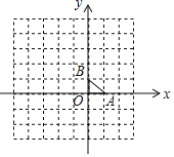
【题目】如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0),点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,且这些对称中心依次循环,已知P1的坐标是(1,1),点P2019的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作)BD是矩形ABCD的对角线,![]() ,
,![]() ,将
,将![]() 绕着点B顺时针旋转
绕着点B顺时针旋转![]() (
(![]() )得到
)得到![]() ,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则
,点A、D的对应点分别为E、F.若点E落在BD上,如图①,则![]() ________.
________.
(探究)当点E落在线段DF上时,CD与BE交于点C.其它条件不变,如图②.
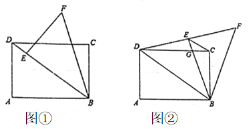
(1)求证:![]() ;
;
(2)CG的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD边长为5,顶点A,B在x轴的正半轴上,顶点D在y轴的正半轴上,且点A的坐标是(3,0),以点C为顶点的抛物线经过点A.

(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若将上述抛物线进行平移,使得平移后的抛物线的顶点P在直线BC上,且此时的抛物线恰好经过点D,求平移后的抛物线解析式及其顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接多边形任意两个不相邻顶点的线段称为多边形的对角线.
(1)
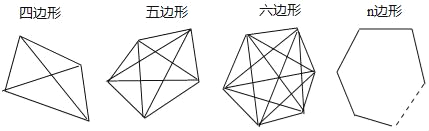
对角线条数分别为 、 、 、 .
(2)n边形可以有20条对角线吗?如果可以,求边数n的值;如果不可以,请说明理由.
(3)若一个n边形的内角和为1800°,求它对角线的条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com