
【题目】如图,菱形ABCD边长为5,顶点A,B在x轴的正半轴上,顶点D在y轴的正半轴上,且点A的坐标是(3,0),以点C为顶点的抛物线经过点A.

(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若将上述抛物线进行平移,使得平移后的抛物线的顶点P在直线BC上,且此时的抛物线恰好经过点D,求平移后的抛物线解析式及其顶点P的坐标.
【答案】(1)点C(5,4);(2)y=﹣(x﹣5)2+4;(3)y=﹣(x﹣2)2﹣8或y=﹣(x+![]() )2+24,点P(2,﹣8)或(﹣
)2+24,点P(2,﹣8)或(﹣![]() ,24).
,24).
【解析】
(1)OA=3,AD=5,则DO=4,故点D(0,4),点C(5,4);
(2)抛物线的表达式为:y=a(x-5)2+4,将点A的坐标代入上式并解得:a=-1,即可求解;
(3)直线BC的表达式为:![]() ;设点P的坐标为:(m,
;设点P的坐标为:(m,![]() ),而点D(0,4),则抛物线的表达式为:y=-(x-m)2
),而点D(0,4),则抛物线的表达式为:y=-(x-m)2![]() ,将点D的坐标代入上式并整理得:3m2+4m-20=0,即可求解.
,将点D的坐标代入上式并整理得:3m2+4m-20=0,即可求解.
(1)OA=3,AD=5,则DO=4,故点D(0,4),点C(5,4);
(2)抛物线的表达式为:y=a(x﹣5)2+4,将点A的坐标代入上式并解得:a=﹣1,
故抛物线的表达式为:y=﹣(x﹣5)2+4;
(3)点A的坐标是(3,0),AB=5,则点B(8,0),将点B、C的坐标代入一次函数表达式y=kx+b得:![]() ,解得:
,解得: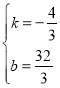 ,
,
故直线BC的表达式为:y=﹣![]() x+
x+![]() ;
;
设点P的坐标为:(m,﹣![]() m+
m+![]() ),而点D(0,4),
),而点D(0,4),
则抛物线的表达式为:y=﹣(x﹣m)2﹣![]() m+
m+![]() ,
,
将点D的坐标代入上式并整理得:3m2+4m﹣20=0,解得:m=2或﹣![]() ,
,
故点P(2,﹣8)或(﹣![]() ,24),
,24),
故抛物线的表达式为:y=﹣(x﹣2)2﹣8或y=﹣(x+![]() )2+24.
)2+24.


科目:初中数学 来源: 题型:
【题目】万州二中八十周年校庆来临之际,学校本着“简朴,节俭,实效,特色”的原则将 2019年 10 月 25 日至 11 月 25 日定为校友回访月,学校总务处购买了红,黄,蓝三种花卉装扮 出 A,B,C,D 四种造型,其中一个 A 造型需要 15 盆红花,10 盆黄花,10 盆蓝花;一个 B 造型需要 5 盆红花,7 盆黄花,6 盆蓝花;一个 C 造型需要 7 盆红花,8 盆黄花,9 盆蓝 花;一个 D 造型需要 7 盆红花,10 盆黄花,10 盆蓝花,若一个 A 造型售价 1800 元,利润 率为 20%,一个 B 和一个 C 造型一共成本和为 1935 元,且一盆红花的利润率为 25%,则一个 D 造型的售价为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
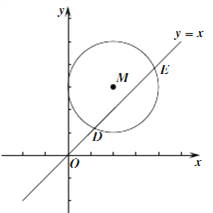
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
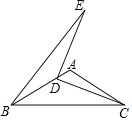
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=2,则△BDE面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(120>x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,月销售额为14000元,此月共盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
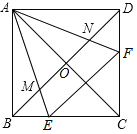
【题目】如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN,以上结论中,正确的是______ .(请把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
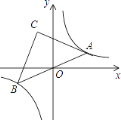
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com