
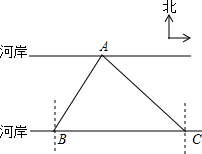
 如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 过点A作AD⊥BC于点D,设AD=xm.用含x的代数式分别表示BD,CD.再根据BD+CD=BC,列出方程$\frac{\sqrt{3}}{3}$x+x=150,解方程即可.
解答 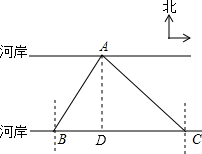 解:过点A作AD⊥BC于点D,设AD=xm.
解:过点A作AD⊥BC于点D,设AD=xm.
在Rt△ABD中,∵∠ADB=90°,∠BAD=30°,
∴BD=AD•tan30°=$\frac{\sqrt{3}}{3}$x.
在Rt△ACD中,∵∠ADC=90°,∠CAD=45°,
∴CD=AD=x.
∵BD+CD=BC,
∴$\frac{\sqrt{3}}{3}$x+x=150,
∴x=75(3-$\sqrt{3}$)≈95.
即A点到河岸BC的距离约为95m.
点评 本题考查了解直角三角形的应用-方向角问题,通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,有公共直角边的可利用这条边进行求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
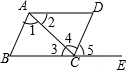 分别根据已知条件进行推理,得出结论,并说明理由.
分别根据已知条件进行推理,得出结论,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com