
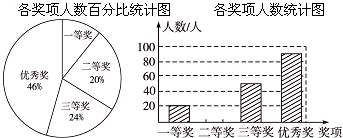
���� ��1������1��ȥ��������İٷֱȼ�����⣻
��2������һ�Ƚ���20�ݣ�ռ10%�����������Ʒ����������Ʒ�����Զ��Ƚ��İٷֱ���ö��Ƚ�������������������ͳ��ͼ����������
��3���������������Ƚ��İٷֱȼ�����û����Ƚ���������
��� �⣺��1��1-20%-24%-46%=10%��
�ʴ��ǣ�10%��
��2���ߴ�����ͳ��ͼ��֪��һ�Ƚ��Ļ�����Ϊ20��
����α������յ��IJ�����ƷΪ$\frac{20}{10%}$=200�ݣ�
����Ƚ��Ļ�����Ϊ200��20%=40��
����ͳ��ͼ��������ͼ��ʾ��
��3�������Ƚ���ѧ���У�200��24%=48�ˣ�
���� ���⿼���������ͳ��ͼ������ͳ��ͼ���ۺ����ã�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | ���� | Ƶ�� | Ƶ�� |
| 1 | 89.5��99.5 | 4 | 0.04 |
| 2 | 99.5��109.5 | 3 | 0.03 |
| 3 | 109.5��119.5 | 46 | 0.46 |
| 4 | 119.5��129.5 | B | c |
| 5 | 129.5��139.5 | 6 | 0.06 |
| 6 | 139.5��149.5 | 2 | 0.02 |
| �ϼ� | a | 1.00 | |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��4��4�ķ����������ͬ����С�������ΰ�ͼʾλ�ðڷţ��ƶ�����һ�������ε��հ����У��������ĸ���������ɵ���ͼ����һ����Գ�ͼ�Σ��������Ʒ��У�����������
��4��4�ķ����������ͬ����С�������ΰ�ͼʾλ�ðڷţ��ƶ�����һ�������ε��հ����У��������ĸ���������ɵ���ͼ����һ����Գ�ͼ�Σ��������Ʒ��У�����������| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com