
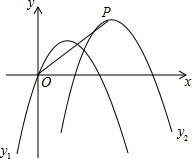
 已知抛物线:y1=-$\frac{1}{2}x^2+2x$
已知抛物线:y1=-$\frac{1}{2}x^2+2x$分析 (1)直接根据抛物线的顶点坐标公式即可得出结论;
(2)根据二次函数平移的性质求出平移后的顶点坐标,进而可得出其解析式;
(3)先判断出N所在的位置,再分点N在抛物线y1上与点N在抛物线y2上两种情况进行讨论.
解答 解:(1)∵依题意a=-$\frac{1}{2}$,b=,2c=0,
∴-$\frac{b}{2a}$=-$\frac{2}{2×(-\frac{1}{2})}$=2,$\frac{4ac-{b}^{2}}{4a}$=$\frac{0-{2}^{2}}{4×(-\frac{1}{2})}$=2,
∴顶点坐标是(2,2);
(2)∵y2解析式中的二次项系数为-$\frac{1}{2}$,且y2的顶点坐标是(4,3)
∴y2=-$\frac{1}{2}$(x-4)2+3,即:y2=-$\frac{1}{2}$x2+4x-5;
(3)符合条件的N点存在
如图:若四边形OPMN为符合条件的平行四边形,则OP∥MN,且OP=MN,∠POA=∠BMN,
作PA⊥x轴于点A,NB⊥x轴于点B,
∴∠PAO=∠MBN=90°,
在△POA与△NMB中,
∵$\left\{\begin{array}{l}∠POA=∠BMN\\∠PAO=∠MBN\\ OP=MN\end{array}\right.$,
∴△POA≌△NMB(AAS),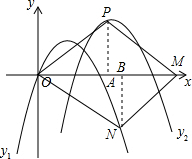
∴PA=BN.
∵点P的坐标为(4,3),
∴NB=PA=3,
∵点N在抛物线y1、y2上,且P点为y1、y2的最高点,
∴符合条件的N点只能在x轴下方
①点N在抛物线y1上,则有:-$\frac{1}{2}$x2+2x=-3
解得:x=2-$\sqrt{10}$或x=2+$\sqrt{10}$,
②点N在抛物线y2上,则有:-$\frac{1}{2}$(x-4)2+3=-3,
解得:x=4-2$\sqrt{3}$或x=4+2$\sqrt{3}$.
∴符合条件的N点有四个:N1(2-$\sqrt{10}$,-3),N2(4-2$\sqrt{3}$,-3),N3(2+$\sqrt{10}$,-3),N4(4+2$\sqrt{3}$,-3).
点评 本题考查的是二次函数综合题,涉及到二次函数图象上点的坐标特点、平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | -$\frac{16}{3}$ | C. | $\frac{16}{5}$ | D. | -$\frac{16}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
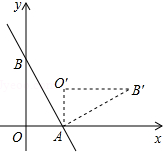 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,求点B′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
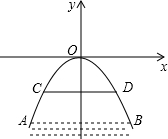 如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?
如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com