
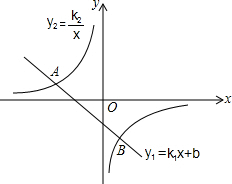 已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.
已知,如图,A(-4,2),B(n,-4)是一次函数y1=k1+b图象与反比例函数y2=$\frac{{k}_{1}}{x}$的图象的两个交点.分析 (1)首先把A(-4,2)代入反比例函数解析式中确定k2,然后把B(n,-4)代入反比例函数的解析式确定n,然后根据A,B两点坐标利用待定系数法确定一次函数的解析式;
(2)根据图象和交点坐标即可求得.
解答 解:(1)把A(-4,2)代入y2=$\frac{{k}_{2}}{x}$中,
∴k2=-8,
∴y=-$\frac{8}{x}$,
把B(n,-4)代入求出的反比例函数解析式中得,n=2,
∴B(2,-4),
把A(-4,2),B(2,-4)代入y1=k1x+b得,
$\left\{\begin{array}{l}{-4{k}_{1}+b=2}\\{2{k}_{1}+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=-2}\end{array}\right.$
∴一次函数解析式为y=-x-2.
(2)由图象可知:使y1>y2的x的取值范围是x<-4或0<x<2.
点评 此题考查了用待定系数法确定反比例函数和一次函数的解析式,需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.


科目:初中数学 来源: 题型:解答题
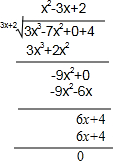 我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们可以用竖式进行演算,即先把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.例如:
我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们可以用竖式进行演算,即先把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.例如:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
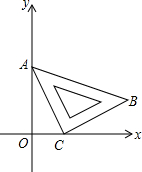 在平面直角坐标系中,将一块为等腰Rt△ABC的三角板按如图所示放置,若AO=2,OC=1,∠ACB=90°.
在平面直角坐标系中,将一块为等腰Rt△ABC的三角板按如图所示放置,若AO=2,OC=1,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
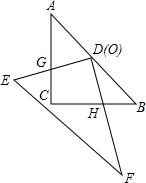 如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.
如图:一幅三角板如图放置,等腰直角△ABC固定不动,另一块△DEF的直角顶点放在等腰直角△ABC的斜边AB中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AC、BC上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
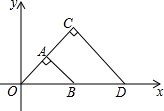 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:4,∠OCD=90°,CO=CD.若点B的坐标为(1,0),则点C的坐标为( )| A. | (2,2) | B. | (2,4) | C. | (2$\sqrt{2},2\sqrt{2}$) | D. | (4,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com