
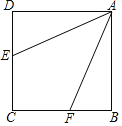
【题目】如图,已知正方形ABCD,点E,F分别在CD,BC上,且∠EAF=∠DAE+∠BAF,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
将△ADE旋转至△ABH,根据旋转的性质可得∠DAE=∠BAH,AE=AH,DE=BH,再利用”SAS“证明△AEF≌△AHF,从而得EF=FH,再根据勾股定理即可求CE2+CF2=EF2,即有(CE﹣CF)2+2CECF=(BF﹣DE)2+4BFDE,而BF﹣DE=CE﹣CF,即可求解.
如图,连接EF,将△ADE旋转至△ABH
∴∠DAE=∠BAH,AE=AH,DE=BH
∴∠EAF=∠DAE+∠BAF=∠BAH+∠BAF=∠FAH
∵∠D=∠ABC=∠ABH=90°
∴∠ABC+∠ABH=180°
∴C,B,H三点共线
∵AF=AF
∴△AEF≌△AHF(SAS)
∴EF=FH=FB+BH=FB+DE
∵DE+CE=CF+BF
∴BF﹣DE=CE﹣CF
∵CE2+CF2=EF2
∴CE2+CF2=(BF+DE)2
∴(CE﹣CF)2+2CECF=(BF﹣DE)2+4BFDE
∵BF﹣DE=CE﹣CF
∴2CECF=4BFDE
∴![]()
故选:A.


科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节前夕,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销量大,店主决定将玫瑰每枝降价2元促销,降价后80元可购买玫瑰的数量是原来可购买玫瑰数量的1.25倍.
(1)试问:降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于1000元的资金再次购进两种鲜花共180枝,康乃馨进价为6元/枝,玫瑰的进价是5元/枝。试问;至少需要购进多少枝玫瑰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任大叔决定在承包的荒山上种樱桃树,第一次用1000元购进了一批树苗,第二次又用1000元购进该种树苗,但这次每棵树苗的进价是第一次进价的2倍,购进数量比第次少了100棵;
(1)求第一次每棵树苗的进价是多少元?
(2)一年后,树苗的成活率为85%,每棵樱桃树平均产樱桃30斤,任大叔将两批樱桃树所产樱桃按同一价格全部销售完毕后,获利不低于89800元,求每斤樱桃的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
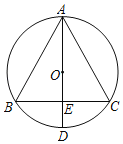
【题目】如图,△ABC内接于⊙O,AD为⊙O的直径,AD与BC相交于点E,且BE=CE.
(1)请判断AD与BC的位置关系,并说明理由;
(2)若BC=6,ED=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD为∠CAB的平分线,点O在AB上,⊙O经过点A,D两点,与AC,AB分别交于点E,F
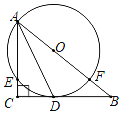
(1)求证:BC与⊙O相切;
(2)若AC=8,AF=10,求AD和BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.
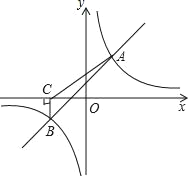
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=ax+b与双曲线![]() 交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
(1)①求k的值和点C的坐标;②求直线l的表达式;
(2)过点B作y轴的垂线与直线AC交于点D,经过点C的直线与直线BD交于点E.若30°≤∠CED≤45°,直接写出点E的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com