
【题目】如图,在Rt△ABC中,∠ACB=90°,AD为∠CAB的平分线,点O在AB上,⊙O经过点A,D两点,与AC,AB分别交于点E,F
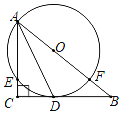
(1)求证:BC与⊙O相切;
(2)若AC=8,AF=10,求AD和BC的长.
【答案】(1)见解析;(2)AD=![]() ,
,![]() .
.
【解析】
(1)连接OD.根据等腰三角形的性质得到∠ODA=∠OAD.根据角平分线的定义得到∠CAD=∠BAD.根据平行线的性质得到∠ODB=∠ACB=90°,于是得到结论;
(2)连接DF.根据圆周角定理得到∠ADF=90°,根据相似三角形的性质得到AD=![]() ,由勾股定理得到CD=
,由勾股定理得到CD=![]() =4.根据相似三角形的性质即可得到结论.
=4.根据相似三角形的性质即可得到结论.
(1)证明:连接OD.
∵OA=OD,
∴∠ODA=∠OAD.
又∵AD平分∠CAB,
∴∠CAD=∠BAD.
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴OD⊥BC,
∴BC与⊙O相切;
(2)解:连接DF.
∵AF为直径,
∴∠ADF=90°,
∴∠ACD=∠ADF.
又∵∠CAD=∠FAD,
∴△CAD∽△DAF,
∴![]() ,
,
∴AD2=CAAF=80,
∴AD=![]() ,
,
在Rt△ACD中,CD=![]() =4.
=4.
∵OD∥AC,
∴△BOD∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() .
.


科目:初中数学 来源: 题型:
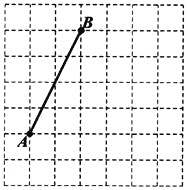
【题目】线段AB在由边长为1的小正方形组成的网格中,端点A、B为格点(即网格线的交点).
(1)线段AB的长度为________;
(2)在网格中找出一个格点C,使得△ABC是以AB为直角边的等腰直角三角形,请画出△ABC;
(3)在网格中找出一个格点D,使得△ABD是以AB为斜边的等腰直角三角形,请画出△ABD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.
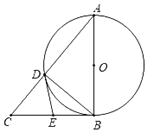
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
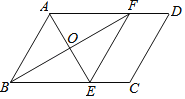
【题目】已知:如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,平行四边形ABCD的面积是36,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
x,l4:y4=﹣![]() x,OA1=1,过点A1作A1A2⊥x轴交l1于点A2,再过点A2作A2A3⊥l1,交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4,……,则点A2020的坐标为_____.
x,OA1=1,过点A1作A1A2⊥x轴交l1于点A2,再过点A2作A2A3⊥l1,交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4,……,则点A2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
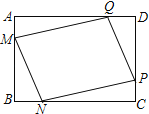
【题目】某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=120,求S的最小值,并求出此时x的值;
(3)若a=200,且每平方米绿化费用需50元,则此时绿化最低费用为______万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是![]() 的直径,AB与
的直径,AB与![]() 相切于点A,四边形ABCD是平行四边形,BC交
相切于点A,四边形ABCD是平行四边形,BC交![]() 于点E.
于点E.

![]() 判断直线CD与
判断直线CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() 的半径为5cm,弦CE的长为8cm,求AB的长.
的半径为5cm,弦CE的长为8cm,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com