
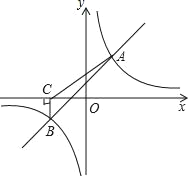
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=x+1.(2)5.
,一次函数的解析式为y=x+1.(2)5.
【解析】
(1)把A的坐标代入反比例函数的解析式,求出其解析式,把B的坐标代入反比例函数的解析式,求出B的坐标,把A、B的坐标代入一次函数的解析式,得出方程组,求出方程组的解即可;
(2)求出BC=|﹣2|=2,BC边上的高是|﹣3|+2,代入三角形的面积公式求出即可.
解:(1)∵点A(2,3)在y=![]() 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为y=![]() ,
,
∴n=![]() =﹣2,
=﹣2,
∵点A(2,3),B(﹣3,﹣2)在y=kx+b的图象上,
∴![]()
∴![]()
∴一次函数的解析式为y=x+1.
(2)以BC为底,则BC边上的高为3+2=5,
S△ABC=![]() ×2×5=5,
×2×5=5,
答:△ABC的面积是5.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:
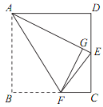
【题目】如图,在正方形纸片 ABCD 中, E 是 CD 的中点,将正方形纸片折叠,点 B 落在线段AE 上的点 G 处,折痕为 AF .若 AD=4 cm,则 CF 的长为___________cm .
查看答案和解析>>
科目:初中数学 来源: 题型:
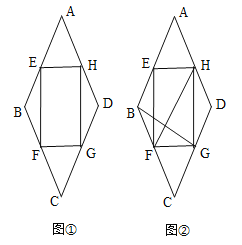
【题目】在菱形ABCD中,∠A=60°,AB=8cm,如图①,点E,H从点A开始向B,D运动,同时点F,G从点C向B,D运动,运动速度都为1cm/秒,运动时间为t秒(0≤t<8).
(1)当运动时间t=4时,求证:四边形EFGH为矩形;
(2)当t等于多少秒时,四边形EFGH面积是菱形ABCD面积的![]() ;
;
(3)如图②,连接HF,BG,当t等于多少秒时,HF⊥BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
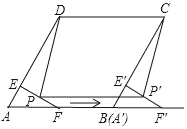
【题目】如图,在菱形ABCD中,∠A=60°,AD=4,点F是AB的中点,过点F作FE⊥AD,垂足为E,将△AEF沿点A到点B的方向平移,得到△A'E'F',设点P、P'分别是EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
A. 7![]() B. 6
B. 6![]() C. 8
C. 8![]() D. 8
D. 8![]() ﹣4
﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
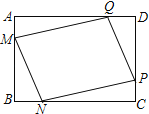
【题目】某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=120,求S的最小值,并求出此时x的值;
(3)若a=200,且每平方米绿化费用需50元,则此时绿化最低费用为______万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
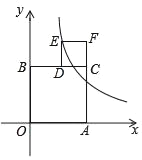
【题目】如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数![]() (k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
(k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外其他都相同,其中标有数字2卡片的张数是标有数字3卡片的张数的3倍少8张.已知从箱子中随机摸出一张标有数字1卡片的概率是![]() .
.
(1)求木箱中装有标1的卡片张数;
(2)求从箱子中随机摸出一张标有数字3的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
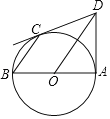
【题目】已知:如图,AB是⊙O的直径,直线DC,DA分别切⊙O于点C,点A,连结BC,OD.
(1)求证:BC∥OD.
(2)若∠ODC=36°,AB=6,求出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com