
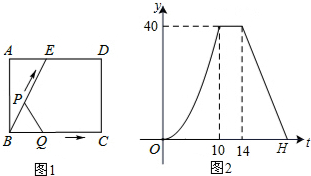
分析 由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:
(1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;
(2)在ED段,y=40是定值,持续时间4s,则ED=4;
(3)在DC段,y持续减小直至为0,y是t的一次函数.
解答 解:(1)分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm,故①正确;
(2)如答图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=10cm,S△BEC=40=$\frac{1}{2}$BC•EF=$\frac{1}{2}$×10×EF,∴EF=8,∴sin∠EBC=$\frac{EF}{BE}$,故②正确;
(3)如答图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=t,
∴y=S△BPQ=$\frac{1}{2}$BQ•PG=$\frac{1}{2}$BQ•BP•sin∠EBC=$\frac{1}{2}$t•t•$\frac{4}{5}$=$\frac{2}{5}$t2.
故③正确;
(4)结论D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如答图3所示,连接NB,NC.
此时AN=8,ND=2,由勾股定理求得:NB=8$\sqrt{2}$,NC=2$\sqrt{17}$,
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
故④错误;
故答案为:①②③.
点评 本题考查动点问题的函数图象,需要结合几何图形与函数图象,认真分析动点的运动过程.突破点在于正确判断出BC=BE=10cm.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
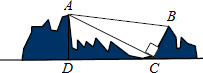 如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)
如图,某景区有一出索道游览山谷的旅游点,已知索道两端距离AB为1300米,在山脚C点测得BC的距离为500米,∠ACB=90°,在C点观测山峰顶点A的仰角∠ACD=23.5°,求山峰顶点A到C点的水平面高度AD.(参考数据:sin23.5°≈0.40,cos23.5°=0.92,tan23.5°=0.43)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
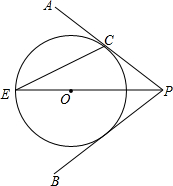 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
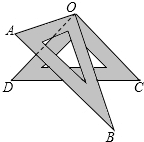 如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )
如图,将一幅三角尺叠放在一起,使直角顶点重合于点O,绕点O任意转动其中一个三角尺,则与∠AOD始终相等的角是( )| A. | ∠BOD | B. | ∠ABO | C. | ∠BOC | D. | ∠BAO |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com