
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM; ②△EOB≌△CMB;③MB:OE=3:2;④四边形EBFD是菱形.其中正确结论是( )
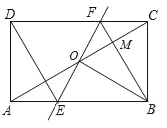
A.①②③B.②③④C.①④D.①③④
【答案】D
【解析】
先证明△BOC是等边三角形,得FO=FC,BO=BC,故①正确;因为△EOB≌△FOB≌△FCB,故△EOB不会全等于△CBM,故②错误;再证明四边形EBFD是平行四边形,由BE=BF推出四边形EBFD是菱形故③正确,设FM=a,则OF=OE=2a,FB=4a,由此推出④正确,由此不难得到答案.
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AO=OC,
∴BO=OC=OA,
∵∠COB=60°,
∴△BCO是等边三角形,
∴∠ACB=∠OBC=60°,BC=OB,
∵FO=FC,BO=BC,
∴FB⊥OC,OM=CM,故①正确,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴故②错误,
∴∠CBM=∠MBO=∠OBA=30°,∠FCO=∠FOC=30°,∠OFB=∠BFC=60°,
∴∠EBF=∠BFE=60°,
∴△EFB是等边三角形,
∴BE=BF,
在△FOC和△EOA中,
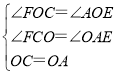 ,
,
∴△FOC≌△EOA(AAS),
∴AE=CF,OE=OF,
∵DC=AB,
∴DF=EB,
∵DF∥EB,
∴四边形EBFD是平行四边形,
∵BE=BF,
∴四边形EBFD是菱形,故③正确,
设FM=a,
在Rt△OFM中,∵∠FOM=30°,
∴OF=2FM=2a,
在Rt△FOB中,∵∠FOB=90°,∠FBO=30°,
∴BF=2OF=4a,
∴BM=3a,
∴BM:OE=3:2,故④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4x+5.
(1)用配方法将y=-x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的发散点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=3r,则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
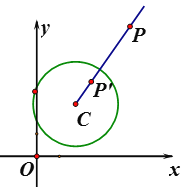
根据上述材料,请你解决以下问题:
(1)当⊙O的半径为1时,
①在点![]() 关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
②点P在直线![]() 上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
(2)⊙C的圆心C在x轴上,半径为1,直线![]() 与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.
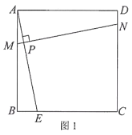
问题探究:在“问题情境”的基础上,
(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;
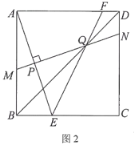
(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.
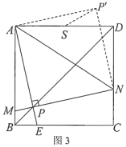
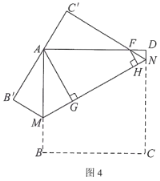
问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=![]() ,请直接写出FH的长.
,请直接写出FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
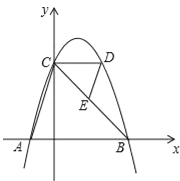
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com