
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的发散点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=3r,则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
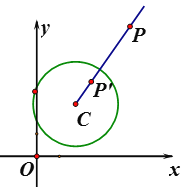
根据上述材料,请你解决以下问题:
(1)当⊙O的半径为1时,
①在点![]() 关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
②点P在直线![]() 上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
(2)⊙C的圆心C在x轴上,半径为1,直线![]() 与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
【答案】(1)N,T ![]() ,(0,0);(2)
,(0,0);(2)![]() <m<3.
<m<3.
【解析】
(1)①根据发散点的定义依次进行判断即可;②由OP≤3r=3,得出OP2≤9,设P(m,![]() ),由勾股定理得出OP2=m2+(
),由勾股定理得出OP2=m2+(![]() )2=4m2-18m+27≤9,解不等式得出
)2=4m2-18m+27≤9,解不等式得出![]() ≤m≤3.再分别将m=
≤m≤3.再分别将m=![]() 与3代入检验即可;
与3代入检验即可;
(2)先由已知条件求出A(9,0),B(0,3![]() ),则
),则![]() ,∠OBA=60°,∠OAB=30°.再设C(n,0),分两种情况进行讨论:①C在OA上;②C在A点右侧.
,∠OBA=60°,∠OAB=30°.再设C(n,0),分两种情况进行讨论:①C在OA上;②C在A点右侧.
解:(1)①设点M(3,1)的发散点为M’,则根据发散点的定义可得:OM+OM’=3,
![]() OM=
OM=![]() =
=![]() ,
,
∴OM’=3-![]() <0.
<0.
故不符合题意,点M(3,1)不存在关于⊙O的发散点.
同理可求得:设点N![]() 关于⊙O的发散点为N’,则
关于⊙O的发散点为N’,则
ON+ON’=3,
∴ON’=3-![]() =
=![]()
∴点N![]() 关于⊙O的发散点N’的坐标为
关于⊙O的发散点N’的坐标为![]() ;
;
设点T(2![]() ,1) 关于⊙O的发散点为T’,
,1) 关于⊙O的发散点为T’,
则OT+OT’=3,
∴OT’=3-![]() =0
=0
∴点T(2![]() ,1) 关于⊙O的发散点为T’的坐标为(0,0)
,1) 关于⊙O的发散点为T’的坐标为(0,0)
故答案为:N,T ![]() ,(0,0);
,(0,0);
![]() 设点P的坐标为(m,
设点P的坐标为(m,![]() ),
),
∵OP≤3,
∴![]() ≤9.
≤9.
∴![]() +
+![]() ≤9
≤9
整理得:![]() -
-![]() ≤0
≤0
解得:![]() ≤m≤3.
≤m≤3.
又∵点P不在轴上,
∴点P的横坐标m的取值范围![]() <m<3;
<m<3;
(2)令y=0,则![]() ,解得x=9,
,解得x=9,
∴A的坐标为(9,0)
令x=0,则y=3![]() ,
,
∴点B的坐标为(0,3![]() ).
).
∴![]() ,
,
∴∠OBA=60°,∠OAB=30°.
设C的坐标为(n,0)
当点C在OA上时,作CD⊥AB于D,则
CD≤CP≤3r=3
∴AC=2CD≤6
∴9-n≤6解得n≥3
当点C在点A右边时,AC的最大值为3.
∴C的横坐标n≤12.
综上所述,圆心C的横坐标的取值范围是![]() ≤m≤3.
≤m≤3.


科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
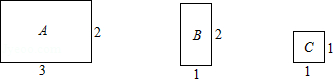
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
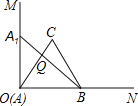
【题目】已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A于点O重合,顶点C在∠MON内部
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法);
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1,试猜想∠BCC1为多少度,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售量,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.
(1)若每件衬衫降价4元,商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点D、E分别是边AB、AC的中点,连接DE,将△ADE绕点A按顺时针方向旋转,记旋转角为α,BD、CE所在直线相交所成的锐角为β.
(1)问题发现当α=0°时,![]() =_____;β=_____°.
=_____;β=_____°.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 和β的大小有无变化?请仅就图2的情形给出证明.
和β的大小有无变化?请仅就图2的情形给出证明.
(3)在△ADE旋转过程中,当DE∥AC时,直接写出此时△CBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
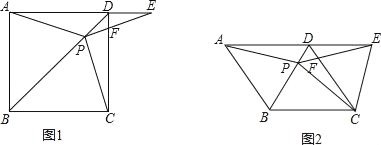
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM; ②△EOB≌△CMB;③MB:OE=3:2;④四边形EBFD是菱形.其中正确结论是( )
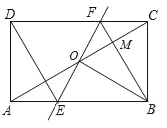
A.①②③B.②③④C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为_____;
(2)P点坐标为______;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
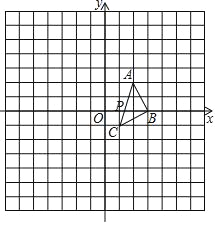
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com