【题目】某商场销售一批名牌衬衫，平均每天可销售20件，每件盈利40元．为了扩大销售量，增加盈利，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价5元，商场平均每天可多售出10件．
(1)若每件衬衫降价4元，商场每天可盈利多少元？
(2)若商场平均每天要盈利1200元，每件衬衫应降价多少元？
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知抛物线与直线的图象如图所示，则下列说法：
①当0＜x＜2时， y1＞y2；②y1随x的增大而增大的取值范围是x＜2；③使得y2大于4的x值不存在；④若y1=2，则x=2﹣
或x=1．其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=-x2+4x+5．
(1)用配方法将y=-x2+4x+5化成y=a（x﹣h）2+k的形式；
(2)指出抛物线的开口方向、对称轴和顶点坐标；
(3)若抛物线上有两点A（x1,y1）,B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为
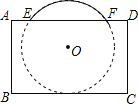
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的发散点的定义如下：若在射线CP上存在一点P′，满足CP＋CP′＝3r，则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地，当点P′与圆心C重合时，规定CP′＝0.
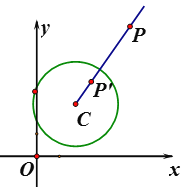
根据上述材料，请你解决以下问题：
（1）当⊙O的半径为1时，
①在点
关于⊙O的发散点的是点 ；其对应发散点的坐标是 ；
②点P在直线
上，若点P关于⊙O的发散点P′存在，且点P′不在x轴上，求点P的横坐标m的取值范围；
（2）⊙C的圆心C在x轴上，半径为1，直线
与x轴、y轴分別交于点A，B.若线段AB上存在点P，使得点P关于⊙C的发散点P′在⊙C的内部，请直接写出圆心C的横坐标n的取值范围 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．
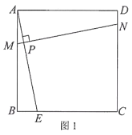
问题探究：在“问题情境”的基础上，
（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；
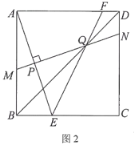
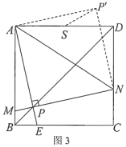
（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P'处．若正方形ABCD的边长为4 ，AD的中点为S，求P'S的最小值．
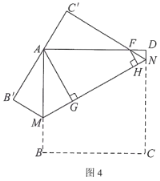
问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG＝
，请直接写出FH的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
