
【题目】二次函数![]() 与一次函数
与一次函数![]() 在一个平面直角坐标系中.
在一个平面直角坐标系中.
(1)若二次函数![]() 的图象顶点在一次函数
的图象顶点在一次函数![]() 上,求
上,求![]() 的值;
的值;
(2)若当![]() 时,二次函数
时,二次函数![]() 的最小值为
的最小值为![]() ,求
,求![]() ,
,![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
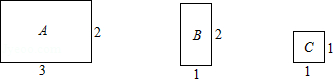
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
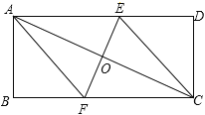
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,EF=6,求菱形AFCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
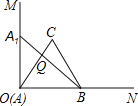
【题目】已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A于点O重合,顶点C在∠MON内部
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法);
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1,试猜想∠BCC1为多少度,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售量,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.
(1)若每件衬衫降价4元,商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com