
【题目】 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
【答案】(1)不是;
(2)54;
(3)![]() .
.
【解析】
(1)根据矩形的性质和“奇妙四边形”的定义进行判断;
(2)连结OB、OD,作OH⊥BD于H,如图2,根据垂径定理,得到BH=DH,根据圆周角定理得到∠BOD=2∠BCD=120°,则利用等腰三角形的性质得∠OBD=30°,在Rt△OBH中可计算出![]() ,
,![]() ,则
,则![]() ,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
(3)连结OB、OC、OA、OD,作OE⊥AD于E,如图3,根据垂径定理得到AE=DE,再利用圆周角定理得到∠BOM=∠BAC,∠AOE=∠ABD,再利用等角的余角相等得到∠OBM=∠AOE,则可证明△BOM≌△OAE得到OM=AE,于是有![]() .
.
解:(1)矩形的对角线相等但不垂直,
所以矩形不是奇妙四边形;
故答案为:不是;
(2)

连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴在等腰△OBD中,∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴![]() ,
,
∴![]()
∴![]()
∵四边形ABCD是奇妙四边形,
∴![]() ,
,![]()
∴![]() ;
;
(3)![]() .
.
理由如下: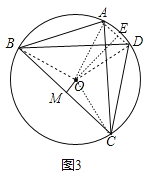
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,
∴在等腰△AOD中,![]() ,
,
又∵![]() ,
,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠/span>AOE,
在△BOM和△OAE中

∴![]() ,
,
∴OM=AE,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的发散点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=3r,则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
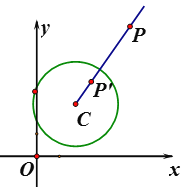
根据上述材料,请你解决以下问题:
(1)当⊙O的半径为1时,
①在点![]() 关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
关于⊙O的发散点的是点 ;其对应发散点的坐标是 ;
②点P在直线![]() 上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围;
(2)⊙C的圆心C在x轴上,半径为1,直线![]() 与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
与x轴、y轴分別交于点A,B.若线段AB上存在点P,使得点P关于⊙C的发散点P′在⊙C的内部,请直接写出圆心C的横坐标n的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
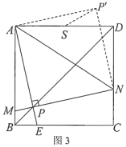
【题目】问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.
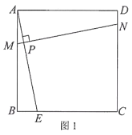
问题探究:在“问题情境”的基础上,
(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;
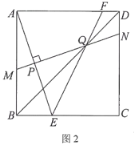
(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.
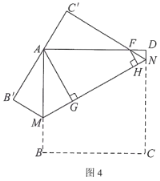
问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=![]() ,请直接写出FH的长.
,请直接写出FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
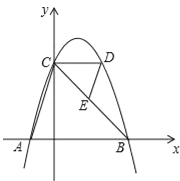
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
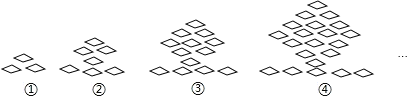
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
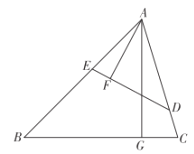
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证ΔADE∽ΔABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com