
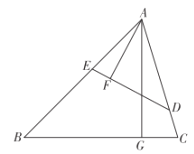
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证ΔADE∽ΔABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90°,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)△ADE∽△ABC,![]() ,又易证△EAF∽△CAG,所以
,又易证△EAF∽△CAG,所以![]() ,即可求解.
,即可求解.
解:(1)证明:在ΔABC中,
∵AG⊥BC于点G,AF⊥DE于点F
∴∠AFE=∠AGC=90°
∵∠EAF=∠GAC
∴∠AED=∠C
在ΔADE和ΔABC中,
∵∠AED=∠C,∠EAD=∠CAB
∴ΔADE∽ΔABC.
(2)解:在ΔAEF和ΔACG中,
∵∠AFE=∠AGC,∠EAF=∠GAC
∴ΔAEF∽ΔAGC
由(1)知ΔADE∽ΔABC
∴![]()
又ΔAEF∽ΔAGC
∴![]()


科目:初中数学 来源: 题型:
【题目】 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
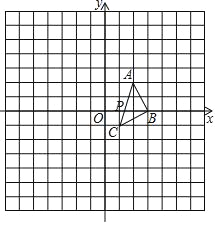
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为_____;
(2)P点坐标为______;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
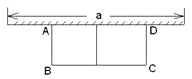
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
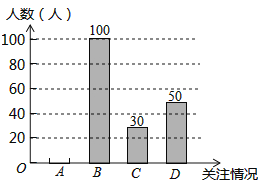
(1)根据上述统计表可得此次采访的人数为 人;m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com