练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

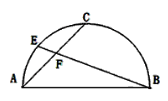
    【题目】如图，AB是半圆的直径，点C是弧AB的中点，点E是弧AC的中点，连结EB、CA交于点F，则 的值为（ ）

    A.B. C. D.

    【答案】D

    【解析】

    先连接OE、BC，利用垂径定理推论，以及圆心角、弧、弦之间的关系，可证得：△ABC、△AMO是等腰直角三角形且OE∥BC，再证△MEF∽△CBF，利用相似三角形的性质即可求出.

    解：取AB中点O，连接OE、BC，OE与AC交于点M．

    ∵AB是半圆的直径, 点C是弧AB的中点，

    ∴∠ACB=90°，则△ABC是等腰直角三角形，

    ∵E为弧AC的中点，

    ∴OE⊥AC，AM=MC，∠AOE=45°，

    ∴OE∥BC，△AMO是等腰直角三角形，

    设OM=1，则AM=1，

    ∴AC=BC=2，OA=，

    ∴OE=，

    ∴EM=

    ∵OE∥BC，

    ∴△MEF∽△CBF，

    ∴，

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

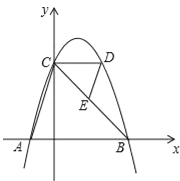
    【题目】如图，抛物线y=﹣（x﹣1）2+4与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，CD∥x轴交抛物线于另一点D，连结AC，DE∥AC交边CB于点E．

    （1）求A，B两点的坐标；

    （2）求△CDE与△BAC的面积之比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售, 已知加工过程中质量损耗了40%, 该商户对该茶叶试销期间, 销售单价不低于成本单价，且每千克获利不得高于成本单价的60%，经试销发现，每天的销售量y（千克）与销售单价x（元/千克）符合一次函数，且x=35时，y=45；x=42时，y=38．

    （1）求一次函数的表达式；

    （2）若该商户每天获得利润(不计加工费用)为W元，试写出利润W与销售单价x之间的关系式；销售单价每千克定为多少元时，商户每天可获得最大利润，最大利润是多少元？

    （3）若该商户每天获得利润不低于225元，试确定销售单价x的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某童装专卖店在销售中发现，一款童装每件进价为40元，若销售价为60元，每天可售出20件，为迎接“双十一”，专卖店决定采取适当的降价措施，以扩大销售量，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件设每件童装降价x元时，平均每天可盈利y元．

    写出y与x的函数关系式；

    当该专卖店每件童装降价多少元时，平均每天盈利400元？

    该专卖店要想平均每天盈利600元，可能吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有长为 24m 的篱笆，现一面利用墙（墙的最大可用长度 a 为 10m）围成中间隔有一道篱笆的长方形花圃，设花圃的宽 AB 为 xm，面积为 Sm2．

    （1） 求 S 与 x 的函数关系式及 x 值的取值范围；

    （2） 要围成面积为 45m2 的花圃，AB 的长是多少米？

    （3） 当 AB 的长是多少米时，围成的花圃的面积最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

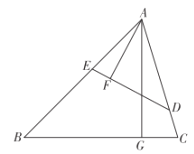
    【题目】如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC.

    （1）求证ΔADE∽ΔABC；

    （2）若AD=3，AB=5，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程m2x2+（2m﹣1）x+1=0有两个不相等的根a，b，

    （1）求实数m的取值范围；

    （2）是否存在实数m，使方程的两个实数根互为相反数？如果存在求出m的值，如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

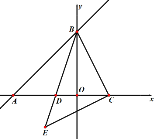
    【题目】如图，直线L：交x轴与点A，交y轴与点B，点C在x轴正半轴上，且OC=2，点D在线段AC上，且∠CDB=∠ABC，过点C作BC的垂线，交BD的延长线与点E，并联结AE

    （1）求证：△CDB∽△CBA

    （2）求点E的坐标

    （3）若点P是直线CE上的一动点，联结DP若△DEP和△ABC相似，求点P的坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．

    （1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=　 　°；

    （2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

    （3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

    查看答案和解析>>

    同步练习册答案