
【题目】某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售, 已知加工过程中质量损耗了40%, 该商户对该茶叶试销期间, 销售单价不低于成本单价,且每千克获利不得高于成本单价的60%,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数![]() ,且x=35时,y=45;x=42时,y=38.
,且x=35时,y=45;x=42时,y=38.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商户每天获得利润(不计加工费用)为W元,试写出利润W与销售单价x之间的关系式;销售单价每千克定为多少元时,商户每天可获得最大利润,最大利润是多少元?
(3)若该商户每天获得利润不低于225元,试确定销售单价x的范围.
【答案】(1)y=-x+80;(2)最大利润为576元;(3)![]()
【解析】
(1)待定系数法求解即可;
(2)先根据加工过程中质量损耗了40%求出宁波白茶的实际成本,再根据“总利润=每千克利润×销售量”列出函数解析式,由“销售单价不低于成本单价,且每千克获利不得高于成本单价的60%”得出x的取值范围,结合二次函数的性质即可求得函数的最值;
(3)根“每天获得利润不低于225元”列出不等式,解不等式后结合![]() 取值,即可解答.
取值,即可解答.
(1)解:将x=35,y=45;x=42,y=38代入![]() ,得:
,得:
![]() ,解得:
,解得:![]()
∴一次函数的表达式为:![]()
(2)∵这批宁波白茶的实际成本为![]() (元/千克)
(元/千克)
∴![]()
∵![]() 即
即![]()
∴当![]() 时,
时,![]()
答:销售单价每千克定为48元时,商户每天可获得最大利润,最大利润是576元.
(3)由题意得:![]()
解得:![]()
又∵![]()
∴![]()


科目:初中数学 来源: 题型:
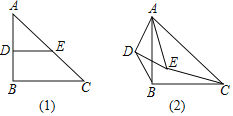
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC=4,点D、E分别是边AB、AC的中点,连接DE,将△ADE绕点A按顺时针方向旋转,记旋转角为α,BD、CE所在直线相交所成的锐角为β.
(1)问题发现当α=0°时,![]() =_____;β=_____°.
=_____;β=_____°.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 和β的大小有无变化?请仅就图2的情形给出证明.
和β的大小有无变化?请仅就图2的情形给出证明.
(3)在△ADE旋转过程中,当DE∥AC时,直接写出此时△CBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2﹣(k+3)x+3图象的对称轴为:直线x=2.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出:
①当y<0时,自变量x的取值范围;
②当0≤x<3时,y的取值范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三江超市为了吸引顾客,设计了一种促销活动,在一个不透明的箱子里放有4个相同小球,在球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客每消费满298元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).超市根据两小球所标金额的和,返还相应价格的购物券.某顾客正好消费298元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券.
(2)请用画树状图或列表的方法,求出该顾客所获得购物券不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
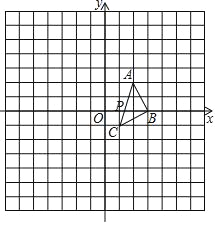
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为_____;
(2)P点坐标为______;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
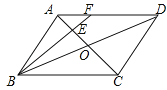
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com