
【题目】已知二次函数y=kx2﹣(k+3)x+3图象的对称轴为:直线x=2.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出:
①当y<0时,自变量x的取值范围;
②当0≤x<3时,y的取值范围是多少?
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4x+5.
(1)用配方法将y=-x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
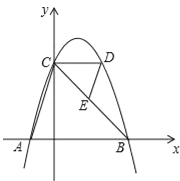
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
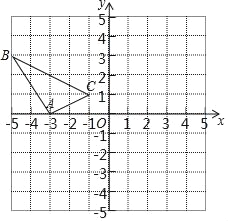
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶经销商以每千克18元的价格购进一批宁波白茶鲜茶叶加工后出售, 已知加工过程中质量损耗了40%, 该商户对该茶叶试销期间, 销售单价不低于成本单价,且每千克获利不得高于成本单价的60%,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数![]() ,且x=35时,y=45;x=42时,y=38.
,且x=35时,y=45;x=42时,y=38.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商户每天获得利润(不计加工费用)为W元,试写出利润W与销售单价x之间的关系式;销售单价每千克定为多少元时,商户每天可获得最大利润,最大利润是多少元?
(3)若该商户每天获得利润不低于225元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
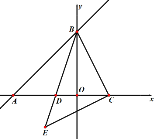
【题目】如图,直线L:![]() 交x轴与点A,交y轴与点B,点C在x轴正半轴上,且OC=2,点D在线段AC上,且∠CDB=∠ABC,过点C作BC的垂线,交BD的延长线与点E,并联结AE
交x轴与点A,交y轴与点B,点C在x轴正半轴上,且OC=2,点D在线段AC上,且∠CDB=∠ABC,过点C作BC的垂线,交BD的延长线与点E,并联结AE
(1)求证:△CDB∽△CBA
(2)求点E的坐标
(3)若点P是直线CE上的一动点,联结DP若△DEP和△ABC相似,求点P的坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com