
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
【答案】(1)△ABC是等腰三角形,理由见解析;(2)△ABC是直角三角形.理由见解析.
【解析】
试题(1)由方程解的定义把x=﹣1代入方程得到a﹣b=0,即a=b,于是由等腰三角形的判定即可得到△ABC是等腰三角形;
(2)由判别式的意义得到△=0,整理得![]() ,然后由勾股定理的逆定理得到△ABC是直角三角形.
,然后由勾股定理的逆定理得到△ABC是直角三角形.
试题解析:解:(1)△ABC是等腰三角形.理由如下:
∵x=﹣1是方程的根,∴(a+c)×1﹣2b+(a﹣c)=0,∴a+c﹣2b+a﹣c=0,∴a﹣b=0,∴a=b,∴△ABC是等腰三角形;
(2)△ABC是直角三角形.理由如下:
∵方程有两个相等的实数根,∴△=![]() ,∴
,∴![]() ,∴
,∴![]() ,∴△ABC是直角三角形.
,∴△ABC是直角三角形.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.

(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2=________,x3=________;
(2)拓展:用“转化”思想求方程![]() =x的解;
=x的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).

(1)当t为何值时,△PBQ是直角三角形?
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;![]() ;
;![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;![]() ;
;![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有![]() 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共![]() 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做![]() 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为![]() 次.
次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
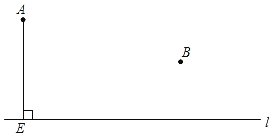
(1)过点B作BF⊥l,垂足为点F;
(2)在直线l上求作一点C,使CA=CB;
(要求:第(1)、(2)小题用尺规作图,并在图中标明相应字母,保留作图痕迹,不写作法.)
(3)在所作的图中,连接CA、CB,若∠ACB=90°,求证:△AEC≌△CFB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC和△AEF中,点E在BC边上,AE=AB,AC=AF,∠CAF=∠BAE,EF与AC交于点G.

(1)求证:EF=BC;
(2)若∠ABC=65°.∠ACB=28°,求∠FGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com