
【题目】解下列方程。
(1)x2-5x+6=0
(2)(2x+1)(x-4)=5.
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
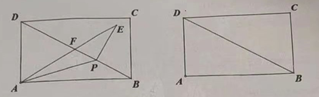
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为对角线
为对角线![]() 上异于点
上异于点![]() 的一个动点,联结
的一个动点,联结![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,使得点
所在的直线翻折,使得点![]() 落在点
落在点![]() 的位置
的位置
(1)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离。
的距离。
(2)联结![]() 交
交![]() 于
于![]() ,求当
,求当![]() 和
和![]() 相似时,线段
相似时,线段![]() 的长。
的长。
(3)当![]() 时,请直接写出此时
时,请直接写出此时![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
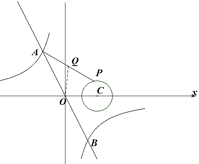
【题目】如图,一次函数y=-2x与反比例函数y=![]() (k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为
(k<0)的图象交于A,B两点,点P在以C(2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
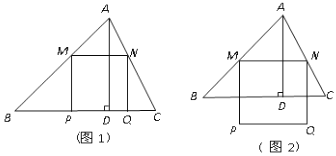
【题目】锐角ΔABC中,BC=6,SΔABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与ΔABC公共部分的面积为y(y>0).
(1)ΔABC中边BC上高AD=______.
(2)当x=______时,PQ恰好落在边BC上(如图1).
(3)当PQ在ΔABC外部时(如图2),求y关于x的函数关系式.(注明x的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
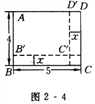
【题目】如图2 - 4所示,长方形ABCD的长为5 cm,宽为4 cm,如果将它的长和宽都减去x(cm),那么它剩下的小长方形AB′C′D′的面积为y(cm2).
(1)写出y与x的函数关系式;
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
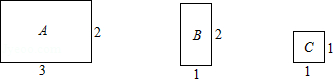
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售量,增加盈利,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价5元,商场平均每天可多售出10件.
(1)若每件衬衫降价4元,商场每天可盈利多少元?
(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com