
����Ŀ�������ABC�У�BC=6��S��ABC=12��������M��N�ֱ��ڱ�AB��AC�ϻ�������MN��BC����MNΪ��������������MPQN������߳�Ϊx��������MPQN����ABC�������ֵ����Ϊy(y>0)��
(1)��ABC�б�BC�ϸ�AD=______.
(2)��x=______ʱ��PQǡ�����ڱ�BC��(��ͼ1).
(3)��PQ����ABC�ⲿʱ(��ͼ2)����y����x�ĺ�����ϵʽ.(ע��x��ȡֵ��Χ)
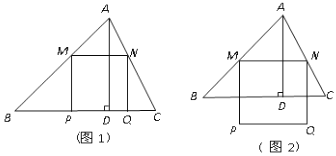
���𰸡�(1)4��(2)2.4��(3)y=4x-![]() x2��(2.4<x<6).
x2��(2.4<x<6).
��������
��1�����������ε������ʽ�������ε������![]() ���ס����㼴�ɣ�
���ס����㼴�ɣ�
��2�����ݡ�AMN���ABC���ƣ����������ζ�Ӧ�ߵıȵ������Ʊ���ʽ���㣻
��3�����������ڡ�ABC�ڵı߳�Ϊa��Ҳ���ǡ�ABC�ĸ����������ڵij��ȣ�Ȼ�����ã�2�������㷽���������a�ij��ȣ������þ��ε������ʽ���н��
��1����S��ABC��12��
��![]() BCAD��12����BC��6��
BCAD��12����BC��6��
��AD��4��
��2����AD��MN�ཻ�ڵ�H��
��MN��BC��
���AMN�ס�ABC��
��![]() ��
��
��![]() ��
��
��ã�x��![]()
�൱x��![]() =2.4ʱ������MPQN�ı�Pǡ������BC���ϣ�
=2.4ʱ������MPQN�ı�Pǡ������BC���ϣ�
��3����MP��NQ�ֱ���BC�ཻ�ڵ�E��F����PQ����ABC���ⲿʱ��x��ȡֵΪ2.4��x��6.
��HD��a����AH��4a��
��![]() ��
��
��![]() ��
��
��ã�a��![]() x��4��
x��4��
�߾���MEFN�������MN��HD��
��y��x��![]() x��4����
x��4����![]() x2��4x��2.4��x��6����
x2��4x��2.4��x��6����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
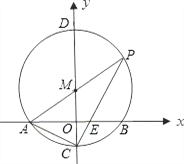
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�M��0�� ![]() ��ΪԲ�ģ���
��ΪԲ�ģ���![]() ��Ϊ�뾶����M��x����A��B���㣬��y����C��D���㣬����AM���ӳ�����M��P�㣬����PC��x����E��
��Ϊ�뾶����M��x����A��B���㣬��y����C��D���㣬����AM���ӳ�����M��P�㣬����PC��x����E��
��1�����CP����ֱ�ߵĽ���ʽ��
��2������AC�������ACP�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���![]()
��1����֤������mȡ��ֵʱ������������������ȵ�ʵ����
��2�������̵�һ����Ϊ1����m��ֵ�����̵���һ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ͼ
��ͼ![]() ����������ABCD�У�
����������ABCD�У�![]() �Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ���
�Ķ���E��F�ֱ���BC��CD���ϣ���AG�������εı߳���ȣ���![]() �Ķ�����
�Ķ�����
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() ��
��![]() ����M��N��BD���ϵ��������㣬��
����M��N��BD���ϵ��������㣬��![]() ����
����![]() �Ƶ�A��ʱ����ת
�Ƶ�A��ʱ����ת![]() ��
��![]() λ�ã�����NH�����ж�MN��ND��DH֮���������ϵ����˵�����ɣ�
λ�ã�����NH�����ж�MN��ND��DH֮���������ϵ����˵�����ɣ�
![]() ��ͼ
��ͼ![]() �У�����BD�ֱ�AE��AF�ڵ�M��N����
�У�����BD�ֱ�AE��AF�ڵ�M��N����![]() ��
��![]() ��
��![]() ����AG��MN�ij���
����AG��MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ��Ļ��˲�ȫ���Ķ�����У�ij��ѧ���š���һ�����硱��ȫУѧ����������ֽ��ͼ���Ķ�������λ�����������˵��飬2012��ȫУ��1000��ѧ����2013��ȫУѧ��������2012������10%��2014��ȫУѧ��������2013������100�ˣ�
��1����2014��ȫУѧ��������
��2��2013��ȫУѧ���˾��Ķ�����2012���1�����Ķ�������2012������1700����ע���Ķ�����=�˾��Ķ�����������
����2012��ȫУѧ���˾��Ķ�����
��2012��������˾��Ķ�����ȫУѧ���˾��Ķ�����2.5�������2012�ꡢ2014��������������˾��Ķ�������ǰһ������һ����ͬ�İٷ���a��2014��ȫУѧ���˾��Ķ�����2012�����ӵİٷ���Ҳ��a����ô2014�������ȫ��80����Ա���Ķ��������ﵽȫУѧ���Ķ�������25%����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС��������Ƶ�ʹ��Ƹ��ʡ���ʵ��ʱ��ͳ����ijһ������ֵ�Ƶ�ʣ���������������ͳ��ͼ���������һ�����ʵ�����п��ܵ��ǣ�������

A. ����װ�д�С���ʵض���ͬ��3�������2�����������ȡһ����ȡ������
B. ��һö�ʵؾ��ȵ������������ӣ����ϵ���ĵ�����ż��
C. �Ⱥ�������һö�ʵؾ��ȵ�Ӳ�ң����ζ����ַ���
D. �Ⱥ�������һö�ʵؾ��ȵ������������ӣ��������ϵ���ĵ���֮����7��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=-x2+4x+5��
(1)���䷽����y=-x2+4x+5����y=a��x��h��2+k����ʽ��
(2)ָ�������ߵĿ��ڷ��Գ���Ͷ������ꣻ
(3)����������������A��x1,y1��,B(x2,y2),���x1>x2>2,�ԱȽ�y1��y2�Ĵ�С.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com