
【题目】如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.

【答案】(1)详见解析;(2)![]() .
.
【解析】
根据直径所对的圆周角是直角即可进行判断BC是⊙O的切线;
连接OD, 利用扇形面积ODE-△OBD=阴影部分的面积,即可求出答案.
证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠A=∠DEB,∠DEB=∠DBC,
∴∠A=∠DBC,
∵∠DBC+∠ABD=90°,
∴BC是⊙O的切线;
(2)连接OD,
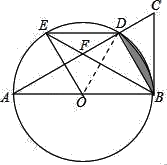
∵BF=BC=2,且∠ADB=90°,
∴∠CBD=∠FBD,
∵OE∥BD,
∴∠FBD=∠OEB,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠CBD=∠OEB=∠OBE=![]() ∠ADB=
∠ADB=![]() 90°=30°,
90°=30°,
∴∠C=60°,
∴AB=![]() BC=2
BC=2![]() ,
,
∴⊙O的半径为![]() ,
,
∴阴影部分的面积=扇形DOB的面积﹣三角形DOB的面积=![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个车间各有工人200人,为了解这两个车间工人的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试,测试成绩如下:
甲:78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙:93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52
整理数据按如下分数段整理、描述这两组样本数据:
50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 | |
甲 | 0 | _____ | 11 | ______ | 1 |
乙 | 1 | 2 | 5 | 10 | ______ |
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
平均数 | 中位数 | 众数 | |
甲 | _____ | 77.5 | 75 |
乙 | 78 | _____ | ______ |
得出结论可以推断_____车间工人的生产技能水平较高,理由为______.(至少从两个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
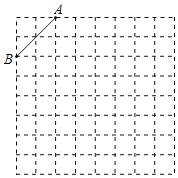
【题目】如图是8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使点A的坐标为(﹣2,4),点B的坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,连接AC,BC,使△BC成为以AB为底的等腰三角形,且腰长是无理数.
①此时点C的坐标为 ,△ABC的周长为 (结果保留根号);
②画出△ABC关于y轴对称的△A′B'C′(点A,B,C的对应点分别A',B',C′),并写出A′,B′,C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
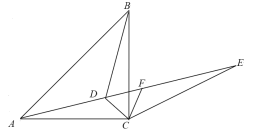
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD.
(1)求证:CD平分∠ACB;
(2)点E是AD延长线上一点,CE=CA,CF∥BD交AE于点F,若∠CAD=15°,
求证:EF=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭轿车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成不完整的条形统计图(图1)和扇形统计图(图2),请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民;
(2)扇形统计图中,C组的百分率是 ;并补全条形统计图;
(3)计算四市中10000名市民上班时最常用家庭轿车的有多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() .
.
![]() 求a的取值范围;
求a的取值范围;
![]() 是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com