
【题目】某工厂甲、乙两个车间各有工人200人,为了解这两个车间工人的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试,测试成绩如下:
甲:78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙:93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52
整理数据按如下分数段整理、描述这两组样本数据:
50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 | |
甲 | 0 | _____ | 11 | ______ | 1 |
乙 | 1 | 2 | 5 | 10 | ______ |
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
平均数 | 中位数 | 众数 | |
甲 | _____ | 77.5 | 75 |
乙 | 78 | _____ | ______ |
得出结论可以推断_____车间工人的生产技能水平较高,理由为______.(至少从两个角度说明推断的合理性)
【答案】填表见解析;甲,①甲车间工人技术水平的平均数比乙车间大②甲车间没有生产技术不合格的工人.
【解析】
利用所有数据的和除以数据个数计算出平均数;把数据按从小到大的顺序排列,由于数字个数是偶数,中间两个数的平均数就是该组数据的中位数,该组数据中出现次数最多的数就是该组数据的众数.
解:由给出的数据可得,甲车间有1人测试成绩在60至69分,7人测试成绩在80至89分;乙车间2人成绩在90分至99分.
甲车间的平均数为:
(78+86+74+85+75+76+87+70+75+90+75+79+81+70+74+80+86+69+83+77)÷20
=78.5;
把乙车间的成绩按从小到大排序为:52,64,67,70,72,73,77,80,80,81,81,81,81,82,83,83,88,93,94
第九、十两数分别为80,81,所以乙车间的中位数为![]() =80.5;出现次数最多的数是81,所以乙车间的众数是81.
=80.5;出现次数最多的数是81,所以乙车间的众数是81.
故答案如下表所示.
50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 | |
甲 | 1 | 7 | |||
乙 | 2 | ||||
平均数 | 中位数 | 众数 | |||
甲 | 78.5 | ||||
乙 | 80.5 | 81 | |||
因为甲车间的人均的平均数高于乙车间,甲车间最低成绩为69分,没有生产技术不合格的工人.
故答案为:甲,①甲车间工人技术水平的平均数比乙车间大②甲车间没有生产技术不合格的工人.(答案不唯一)


科目:初中数学 来源: 题型:
【题目】如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() (千来)与时间
(千来)与时间![]() (小时)之间的关系.
(小时)之间的关系.
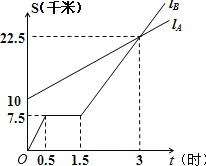
(1)![]() 出发时与
出发时与![]() 相距______千米.
相距______千米.
(2)![]() 走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)![]() 出发后______小时与
出发后______小时与![]() 相遇.
相遇.
(4)求出![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(5)若![]() 的自行车不发生故障,保持出发时的速度前进,那么几小时与
的自行车不发生故障,保持出发时的速度前进,那么几小时与![]() 相遇?相遇点离
相遇?相遇点离![]() 的出发点多少千米?请同学们在图中画出这个相遇点
的出发点多少千米?请同学们在图中画出这个相遇点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
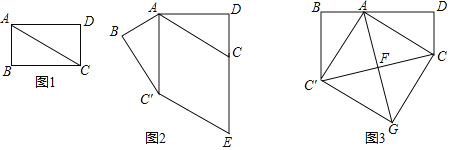
【题目】如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.
(2)若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
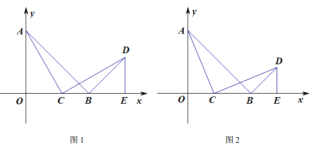
(1)求证:![]() ;
;
(2)猜想![]() 的形状并证明结论;
的形状并证明结论;
(3)如图2,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com