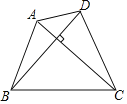
【题目】如图，四边形ABCD中，AC＝BC＝BD，且AC⊥BD，若AB＝a，则△ABD的面积为_____．（用含a的式子表示）
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
【题目】某工厂甲、乙两个车间各有工人200人，为了解这两个车间工人的生产技能情况，进行了抽样调查，过程如下，请补充完整.
收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试，测试成绩如下：
甲：78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙：93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52
整理数据按如下分数段整理、描述这两组样本数据：
50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 | |
甲 | 0 | _____ | 11 | ______ | 1 |
乙 | 1 | 2 | 5 | 10 | ______ |
(说明：成绩80分及以上为生产技能优秀，70～79分为生产技能良好，60～69分为生产技能合格，60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示：
平均数 | 中位数 | 众数 | |
甲 | _____ | 77.5 | 75 |
乙 | 78 | _____ | ______ |
得出结论可以推断_____车间工人的生产技能水平较高，理由为______.(至少从两个角度说明推断的合理性)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程
有两个不相等的实数根
，
．
求a的取值范围；
是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠BDA=∠CDA，则不一定能使△ABD≌△ACD的条件是（ ）
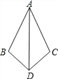
A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AH⊥BC，垂足为H，D为直线BC上一动点(不与点BC重合)，在AD的右侧作△ADE，使得AE=AD，∠DAE=∠BAC，连接CE.
(1)当D在线段BC上时,求证:△BAD≌△CAE；
(2)当点D运动到何处时，AC⊥DE，并说明理由；
(3)当CE∥AB时，若△ABD中最小角为20°，试探究∠ADB的度数(直接写出结果，无需写出求解过程).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程．
已知：如图 1，线段 a 和线段 b．
求作：△ABC，使得 AB = AC，BC = a，BC 边上的中线为 b．
作法：如图 ，
① 作射线 BM，并在射线 BM 上截取 BC = a；
② 作线段 BC 的垂直平分线 PQ，PQ 交 BC 于 D；
③ 以 D 为圆心，b 为半径作弧，交 PQ 于 A；
④ 连接 AB 和 AC．
则△ABC 为所求作的图形．
根据上述作图过程，回答问题：
（1）用直尺和圆规，补全图 2 中的图形；
（2）完成下面的证明：
证明：由作图可知 BC = a，AD = b．
∵ PQ 为线段 BC 的垂直平分线，点 A 在 PQ 上，
∴ AB = AC（ ）（填依据）．
又∵线段 BC 的垂直平分线 PQ 交 BC 于 D，
∴ BD=CD．（ ）（填依据）．
∴ AD 为 BC 边上的中线，且 AD = b．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
