
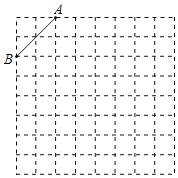
【题目】如图是8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使点A的坐标为(﹣2,4),点B的坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,连接AC,BC,使△BC成为以AB为底的等腰三角形,且腰长是无理数.
①此时点C的坐标为 ,△ABC的周长为 (结果保留根号);
②画出△ABC关于y轴对称的△A′B'C′(点A,B,C的对应点分别A',B',C′),并写出A′,B′,C′的坐标.
【答案】(1)见解析;(2)①(﹣1,1),2![]() +2
+2![]() ;②作图见解析,A′(2,4),B′(4,2),C′(1,1).
;②作图见解析,A′(2,4),B′(4,2),C′(1,1).
【解析】
(1)根据A点的坐标,即可确定坐标系的位置;
(2)①在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,则C一定在AB的中垂线上,通过作图即可确定C的位置;根据勾股定理即可求得三角形的周长;②依据轴对称的性质,即可得到△ABC关于y轴对称的△A'B'C',即可得到A′,B′,C′的坐标.
解:(1)如图,平面直角坐标系如下:

(2)①如图,C点坐标为(﹣1,1),
AB=![]() =2
=2![]() ,BC=AC=
,BC=AC=![]() =
=![]() ,
,
所以△ABC的周长是2![]() +2
+2![]() .
.
故答案为(﹣1,1),2![]() +2
+2![]() ;
;
②如图,△A'B'C'即为所求,A′(2,4),B′(4,2),C′(1,1).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 经过点M(1,3)和N(3,5)
经过点M(1,3)和N(3,5)

(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别表示
分别表示![]() 步行与
步行与![]() 骑车在同一路上行驶的路程
骑车在同一路上行驶的路程![]() (千来)与时间
(千来)与时间![]() (小时)之间的关系.
(小时)之间的关系.
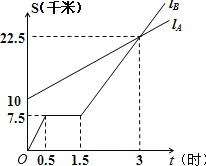
(1)![]() 出发时与
出发时与![]() 相距______千米.
相距______千米.
(2)![]() 走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)![]() 出发后______小时与
出发后______小时与![]() 相遇.
相遇.
(4)求出![]() 行走的路程
行走的路程![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(5)若![]() 的自行车不发生故障,保持出发时的速度前进,那么几小时与
的自行车不发生故障,保持出发时的速度前进,那么几小时与![]() 相遇?相遇点离
相遇?相遇点离![]() 的出发点多少千米?请同学们在图中画出这个相遇点
的出发点多少千米?请同学们在图中画出这个相遇点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
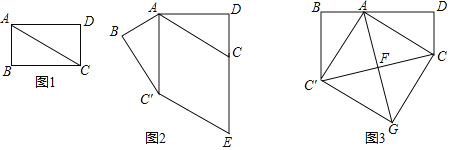
【题目】如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.
(2)若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
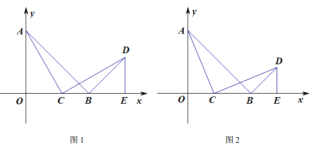
(1)求证:![]() ;
;
(2)猜想![]() 的形状并证明结论;
的形状并证明结论;
(3)如图2,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.
(1)求证:BC是⊙O的切线;
(2)若BF=BC=2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,用配方法求最值.
已知a,b为非负实数,∵a+b﹣2![]() =(
=(![]() )2+(
)2+(![]() )2﹣2
)2﹣2![]() =(
=(![]() ﹣
﹣![]() )2≥0,∴a+b≥2
)2≥0,∴a+b≥2![]() ,当且仅当“a=b”时,等号成立.示例:当x>0时,求y=x+
,当且仅当“a=b”时,等号成立.示例:当x>0时,求y=x+![]() +1的最小值;
+1的最小值;
解:y=(x+![]() )+1>2
)+1>2![]() =3,当x=
=3,当x=![]() ,即x=1时,y的最小值为3.
,即x=1时,y的最小值为3.
(1)探究:当x>0时,求y=![]() 的最小值;
的最小值;
(2)问题解决:随着人们生活水平的提高,汽车已成为越来越多家庭的交通工具,假设某种汽车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养,维修费用总和为![]() 万元,问这种汽车使用多少年报废最合算(即使用多少年的年平均费用最少,年平均费用=所有费用:年数n)?最少年平均费用为多少万元?
万元,问这种汽车使用多少年报废最合算(即使用多少年的年平均费用最少,年平均费用=所有费用:年数n)?最少年平均费用为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com