
����Ŀ���Ķ����ϣ����䷽������ֵ��
��֪a��bΪ�Ǹ�ʵ������a+b��2![]() =��
=��![]() ��2+��
��2+��![]() ��2��2
��2��2![]() =��
=��![]() ��
��![]() ��2��0����a+b��2
��2��0����a+b��2![]() �����ҽ�����a=b��ʱ���Ⱥų�����ʾ������x��0ʱ����y=x+
�����ҽ�����a=b��ʱ���Ⱥų�����ʾ������x��0ʱ����y=x+![]() +1����Сֵ��
+1����Сֵ��
�⣺y=��x+![]() ��+1��2
��+1��2![]() =3����x=
=3����x=![]() ����x=1ʱ��y����СֵΪ3��
����x=1ʱ��y����СֵΪ3��
��1��̽������x��0ʱ����y=![]() ����Сֵ��
����Сֵ��
��2����������������������ˮƽ����ߣ������ѳ�ΪԽ��Խ���ͥ�Ľ�ͨ���ߣ�����ij�������Ĺ�������Ϊ10��Ԫ��ÿ��Ӧ�ɱ��շѵȸ�����ù���0.4��Ԫ��n��ı�����ά�����ܺ�Ϊ![]() ��Ԫ������������ʹ�ö����걨������㣨��ʹ�ö��������ƽ���������٣���ƽ������=���з��ã�����n����������ƽ������Ϊ������Ԫ��
��Ԫ������������ʹ�ö����걨������㣨��ʹ�ö��������ƽ���������٣���ƽ������=���з��ã�����n����������ƽ������Ϊ������Ԫ��
���𰸡���1��x=1ʱ��y����СֵΪ5����2��n=10ʱ����������ʹ��10�걨������㣬������ƽ������Ϊ2.5��Ԫ��
��������
��1�����Ƚ�ԭʽ��Ϊ![]() ��Ȼ��Ӧ���䷽���������x>0ʱ��ԭʽ����Сֵ����.
��Ȼ��Ӧ���䷽���������x>0ʱ��ԭʽ����Сֵ����.
��2�����ȸ������⣬�����ƽ�����ã�Ȼ��Ӧ�������䷽�����������С�γ�ʹ�ö����걨������㣬�Լ�������ƽ������Ϊ������Ԫ����.
��1��y=![]() =x+3+
=x+3+![]() ��2
��2![]() +3=5��
+3=5��
�൱x=![]() ����x=1ʱ��y����СֵΪ5��
����x=1ʱ��y����СֵΪ5��
��2����ƽ������=��![]() +0.4n+10����n=
+0.4n+10����n=![]() +
+![]() +
+![]() ��2
��2![]() +
+![]() =
=![]() =2+0.5=2.5��
=2+0.5=2.5��
�൱![]() =
=![]() ʱ��
ʱ��
��n=10ʱ����������ʹ��10�걨������㣬������ƽ������Ϊ2.5��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
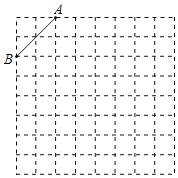
����Ŀ����ͼ��8��8�������������������������а�����Ҫ�������
��1���������н���ƽ��ֱ������ϵ��ʹ��A������Ϊ����2��4������B������Ϊ����4��2����
��2���ڵڶ������ڵĸ���ϻ�һ��C������AC��BC��ʹ��BC��Ϊ��ABΪ�ĵ��������Σ�����������������
�ٴ�ʱ��C������Ϊ�� ������ABC���ܳ�Ϊ�� ��������������ţ���
�ڻ�����ABC����y��ԳƵġ�A��B'C������A��B��C�Ķ�Ӧ��ֱ�A'��B'��C��������д��A����B����C�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
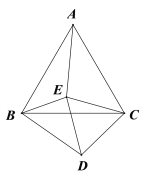
����Ŀ����ͼ��ABC���CDE���ǵȱ�������,�ҡ�EBD=65��,���AEB�Ķ�����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
![]() ��֤��
��֤��![]() ��
��![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ��
��![]() ����
����![]() �İ뾶��
�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��AH��BC������ΪH��DΪֱ��BC��һ����(�����BC�غ�)����AD���Ҳ�����ADE��ʹ��AE=AD����DAE=��BAC������CE.
(1)��D���߶�BC��ʱ,��֤:��BAD�ա�CAE��
(2)����D�˶����δ�ʱ��AC��DE����˵�����ɣ�
(3)��CE��ABʱ������ABD����С��Ϊ20������̽����ADB�Ķ���(ֱ��д�����������д��������).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��AE�ֱ��ǡ�ABC�Ľ�ƽ���ߺ��ߣ���B��45�㣬��C��73�㣮
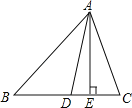
��1�����ADB�Ķ�����
��2�����DAE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����������ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() .������������
.������������![]() �ڵ�һ�����ڵ�ͼ������ABC�й����㣬��k��ȡֵ��Χ��__________.
�ڵ�һ�����ڵ�ͼ������ABC�й����㣬��k��ȡֵ��Χ��__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�������13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�240ǧ�ˣ�
С�죺ͨ��������֤���ҷ���ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮�����һ�κ�����ϵ��ÿ������200ǧ�����ϣ�
��1����ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2���ó�����������ˮ��ÿ���ȡ������ﵽ1040Ԫ����ô���۵���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬С��һ��һ��ȥ���Σ���ͼ��С����Ƶ�ij���ξ����ͼֽ(����������ͬ��С��������ɵģ���С�����εı߳�����ʵ�ʳ���100m)���ڸ�ͼֽ�Ͽɿ���������־�Ծ���A��B.�������ʵ���ƽ��ֱ������ϵ�����A(��3��1)��B(��3����3)������������C(3��2)��λ��������
(1)����ͼ�б������C��λ�ã�
(2)С����Ӿ���B��ʼ���棬;������A����ᄚ��C����С��һ����̵�����·��(�ο����ݣ�![]() ��6�������������)��
��6�������������)��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com