
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

(1)30°;(2)4.
【解析】
试题分析:(1)根据平行线的性质可得∠EDC=∠B=60,根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据含30度角的直角三角形的性质即可求解.
试题解析:【解析】
(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°.
∴∠F=90°﹣∠EDC=30°.
(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形.
∴ED=DC=2.
∵∠DEF=90°,∠F=30°,∴DF=2DE=4.
考点:1.等边三角形的判定与性质;2.平行的性质;3.含30度角的直角三角形的性质.


科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:选择题
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= AB中,一定正确的是( )
AB中,一定正确的是( )

A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:填空题
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=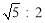 .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:选择题
20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,列方程组正确的是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com