
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=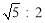 .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .

12或4.
【解析】
试题分析:如答图,过点G作GN⊥AB,垂足为N,连接OE,∴EN=NF,
又∵EG:EF=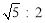 ,∴EG:EN=
,∴EG:EN=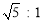 ,
,
又∵GN=AD=8,∴设EN=k,则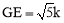 ,根据勾股定理得:
,根据勾股定理得: .
.
解得:k =4.∴EN=4,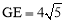 .
.
设⊙O的半径为r,由OE2=EN2+ON2,即:r2=16+(8﹣r)2,解得:r=5.
∵∠GEB为锐角,∴点F在点E的右边,分两种情况:
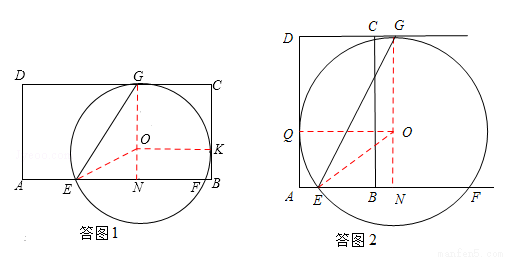
①当边BC所在的直线与⊙O相切于点K时,如答图1,连接OK.∴OK=NB=5.∴EB=9,
又AE=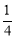 AB,∴AB=12.
AB,∴AB=12.
②当边AD所在的直线与⊙O相切于点Q时,如答图2,连接OQ。∴OQ=AN=5.∴AE=1.
又AE=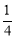 AB,∴AB=4.
AB,∴AB=4.
综上所述,当边AD或BC所在的直线与⊙O相切时,AB的长是12或4.
考点:1.矩形的性质;2.切线的性质;3.勾股定理;4.垂径定理;5.分类思想的应用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则 的长为( )
的长为( )

A. π B. 6π C. 3π D. 1.5π
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:解答题
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:选择题
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√,×,×”,如图1.
(1)若将卡片无标记的一面朝上摆在桌上再分别从两组卡片中随机各抽取一张,求两张卡片上标记都是“√”的概率.(请用“树形图法”或“列表法“求解)
(2)若把A,B两组卡片无标记的一面对应粘贴在一起得到三张卡片,其正、反面标记如图2所示,将卡片正面朝上摆在桌上,并用瓶盖盖住标记.
①若随机揭开其中一个盖子,看到的标记是“√”的概率是多少?
②若揭开盖子,看到的卡片正面标记是“√”后,猜想它的反面也是“√”,求猜对的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com