
有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上“√,×,×”,如图1.
(1)若将卡片无标记的一面朝上摆在桌上再分别从两组卡片中随机各抽取一张,求两张卡片上标记都是“√”的概率.(请用“树形图法”或“列表法“求解)
(2)若把A,B两组卡片无标记的一面对应粘贴在一起得到三张卡片,其正、反面标记如图2所示,将卡片正面朝上摆在桌上,并用瓶盖盖住标记.
①若随机揭开其中一个盖子,看到的标记是“√”的概率是多少?
②若揭开盖子,看到的卡片正面标记是“√”后,猜想它的反面也是“√”,求猜对的概率.

(1)P=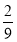 ;
;
(2)①P=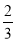 ;
;
②P=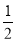 .
.
【解析】
试题分析:(1)先列表,找到所有可能的情况,然后找到满足条件情况,利用概率公式即可求得
(2)①根据题意得到所有等可能情况有3种,其中看到的标记是“√”的情况有2种,即可求出所求概率;
②所有等可能的情况有2种,其中揭开盖子,看到的卡片正面标记是“√”后,它的反面也是“√”的情况有1种,即可求出所求概率.
试题解析:(1)列表如下:
| √ | × | √ |
√ | (√,√) | (×,√) | (√,√) |
× | (√,×) | (×,×) | (√,×) |
× | (√,×) | (×,×) | (√,×) |
所有等可能的情况有9种,两种卡片上标记都是“√”的情况有2种,则P=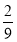 ;
;
(2)①所有等可能的情况有3种,其中随机揭开其中一个盖子,看到的标记是“√”的情况有2种,则P=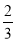 ;
;
②所有等可能的情况有2种,其中揭开盖子,看到的卡片正面标记是“√”后,它的反面也是“√”的情况有1种,则P=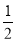 .
.
考点:列表法与树状图法.


科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:填空题
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=
AB,⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线相交于另一点F,且EG:EF=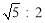 .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:解答题
如图,已知二次函数 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线 ,并写出当
,并写出当 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江宁波卷)数学(解析版) 题型:选择题
菱形的两条对角线长分别是6和8,则此菱形的边长是
A. 10 B. 8 C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:解答题
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江西南昌卷)数学(解析版) 题型:选择题
如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com