练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

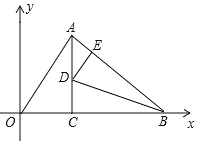
    【题目】如图，△AOB的边OB在x轴上，AC⊥x轴于C，D为AC上一点，将△CBD沿BD翻折，使点C落在AB边上的E点．已知∠AOB＝60°，AO＝4，点B的坐标为（8+2，0），则点D的坐标为_____．

    【答案】

    【解析】

    解直角三角形求出AC，BC，AB，设DC=DE=m．在Rt△ADE中，根据AD2=AE2+DE2，构建方程即可解决问题．

    ∵AC⊥OB，∴∠ACO=90°．

    ∵OA=4，∠AOC=60°，∴∠OAC=30°，∴OCOA=2，ACOC=6．

    ∵B（8+2，0），∴OB=8+2，∴BC=8．

    在Rt△ACB中，AB10，由翻折可知：DC=DE，BC=BE=8，∴AE=2，设DC=DE=m．在Rt△ADE中，∵AD2=AE2+DE2，∴（6﹣x）2=x2+22，解得：x，∴D（2）．

    故答案为：（2）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若点（﹣2，y1），（﹣1，y2），（1，y3）在反比例函数y=的图象上，则下列说法正确的是（ ）

    A．y1＞y2＞y3 B．y3＞y2＞y1 C．y3＞y1＞y2 D．y2＞y1＞y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某市郊外景区内一条笔直的公路a经过三个景点A、B、C，景区管委会又开发了风景优美的景点D，经测量景点D位于景点A的北偏东30°方向8km处，位于景点B的正北方向，还位于景点C的北偏西75°方向上，已知AB=5km．

    （1）景区管委会准备由景点D向公路a修建一条距离最短的公路，不考虑其它因素，求出这条公路的长；（结果精确到0.1km）

    （2）求景点C与景点D之间的距离．（结果精确到1km）

    （参考数据： =1.73， =2.24，sin53°=cos37°=0.80，sin37°=cos53°=0.60，tan53°=1.33，tan37°=0.75，sin38°=cos52°=0.62，sin52°=cos38°=0.79，tan38°=0.78，tan52°=1.28，sin75°=0.97，cos75°=0.26，tan75°=3.73．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校墙边有两根木杆．

    (1)某一时刻甲木杆在阳光下的影子如图所示，你能画出乙木杆的影子吗？(用线段表示影子)

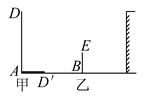
    (2)当乙木杆移动到什么位置时，其影子刚好不落在墙上？

    (3)在你所画的图中有相似三角形吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校墙边有两根木杆．

    (1)某一时刻甲木杆在阳光下的影子如图所示，你能画出乙木杆的影子吗？(用线段表示影子)

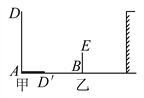
    (2)当乙木杆移动到什么位置时，其影子刚好不落在墙上？

    (3)在你所画的图中有相似三角形吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解某学校八年级学生每周平均体育锻炼时间的情况，随机抽查了该年级的部分学生，对其每周锻炼时间进行统计，根据统计数据绘制成图1和图2两个不完整的统计图．请你根据统计图提供的信息，回答下列问题：

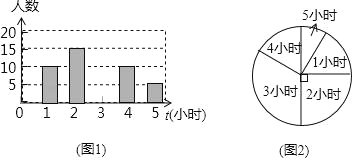
    （1）本次共抽取了学生　 　人，并请将图1条形统计图补充完整；

    （2）这组数据的中位数是　 　，求出这组数据的平均数；

    （3）若八年级有学生1800人，请你估计体育锻炼时间为3小时的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．

    解：∵∠1+∠EFD=180°（邻补角定义），∠1+∠2=180°（已知　）

    ∴　 　（同角的补角相等）①

    ∴　 　（内错角相等，两直线平行）②

    ∴∠ADE=∠3（　 　）③

    ∵∠3=∠B（　 　）④

    ∴　 　（等量代换）⑤

    ∴DE∥BC（　 　）⑥

    ∴∠AED=∠C（　 　）⑦

    查看答案和解析>>

    科目：初中数学 来源： 题型：

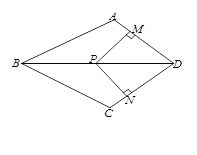
    【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC， P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M、N.

    （1）求证：∠ADB=∠CDB；

    (2)若∠ADC=90°，求证：四边形MPND是正方形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用洗衣粉洗衣物时，漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系，寄宿生小红和小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服，漂洗时，小红每次用一盆水（约10升），小敏每次用半盆水（约5升）．如果她们都用了5克洗衣粉，第一次漂洗后，小红的衣服中残留的洗衣粉还有1.5克，小敏的衣服中残留的洗衣粉还有2克．

    (1)请帮助小红和小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x之间的函数关系式

    (2)当洗衣粉的残留量降至0.5克时，便视为衣服漂洗干净，从节约用水的角度来看，你认为谁的漂洗方法值得提倡？为什么？

    查看答案和解析>>

    同步练习册答案