
【题目】某校墙边有两根木杆.
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
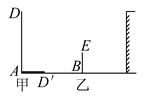
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
【答案】(1)画图见解析;(2)见解析;(3)有,△ADD′与△BEE′相似.
【解析】试题分析:(1)连接甲木杆影子的顶端和甲木杆的顶端DD′就是光线的位置,同时太阳光线是平行的,经过点E作DD′的平行线交AB于点E′即可画出乙木杆的影子;
(2)平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚即可;
(3)利用相似三角形的判定找出相似三角形.
试题解析:
解:(1)如答图1,连接DD′,过E点作直线DD′的平行线,交AD′所在直线于E′,则BE′为乙木杆的影子;
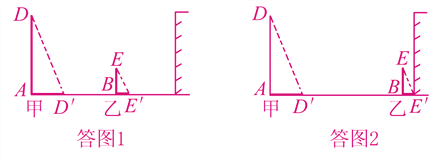
(2)如答图2,平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚;
(3)有,△ADD′与△BEE′相似.
∵DD′∥EE′,
∴∠DD′A=∠EE′B ,
又∵∠DAD′=∠EBE′,
∴△ADD′∽△BEE′(两角对应相等,两三角形相似).


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】某地要建一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.如图建立平面直角坐标系,已知A(![]() ),顶点P(
),顶点P(![]() )
)
(1) 求抛物线的解析式
(2) 若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对八年级学生上学的4种方式:骑车、步行、乘车、接送,进行抽样调查,结果如图(1)、图(2).
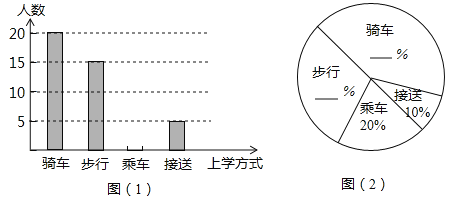
(1)该抽样调查中样本容量是__________,其中,步行人数占样本容量的____%,骑车人数占样本容量的____%,乘车人数占样本容量的____%.
(2)请把条形统计图补充完整;
(3)根据调查结果,你估计该校八年级500名学生中,大约有多少名学生是由家长接送上学的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
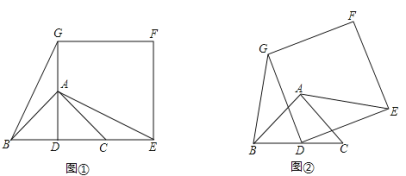
【题目】如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一角度α后(0°<α<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;
(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度α (0°<α<360°)过程中,当BG为最小值时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
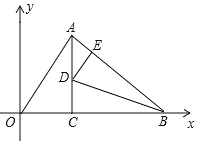
【题目】如图,△AOB的边OB在x轴上,AC⊥x轴于C,D为AC上一点,将△CBD沿BD翻折,使点C落在AB边上的E点.已知∠AOB=60°,AO=4![]() ,点B的坐标为(8+2
,点B的坐标为(8+2![]() ,0),则点D的坐标为_____.
,0),则点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
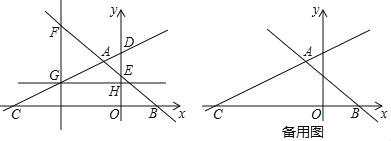
【题目】如图,在平面直角坐标系中,直线AB:y=﹣![]() x+
x+![]() 与直线AC:y=
与直线AC:y=![]() +8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
(1)求点A的坐标;
(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;
(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在平面直角坐标系中,二元一次方程x-y=0的一个解![]() 可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
直线x-y=0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M(x0,y0)的坐标满足不等式x-y≤0,那么点M(x0,y0)就在直线x-y=0的上方区域内。特别地,x=k(k为常数)表示横坐标为k的点的全体组成的一条直线,y=m(m为常数)表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料,探索完成以下问题:
(1)已知点A(2,1)、B(![]() ,
,![]() )、C(
)、C(![]() ,
,![]() )、D(4,
)、D(4,![]() ),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
(2)已知点P(x,y)的坐标满足不等式组![]() ,则所有的点P组成的图形的面积是 ;
,则所有的点P组成的图形的面积是 ;
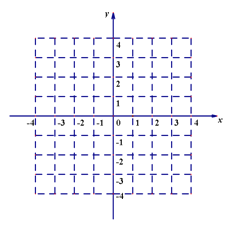
(3)已知点P(x,y)的坐标满足不等式组 ,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com