
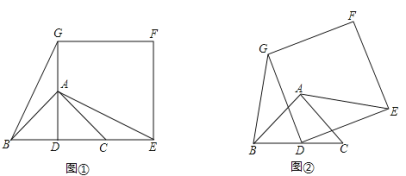
ЁОЬтФПЁПШчЭМ(1)ЃЌвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃН90ЁуЃЌЕуDЪЧBCЕФжаЕуЃЎзїе§ЗНаЮDEFGЃЌЪЙЕуAЁЂCЗжБ№дкDGКЭDEЩЯЃЌСЌНгAEЁЂBGЃЎ
ЃЈ1ЃЉЪдВТЯыЯпЖЮBGКЭAEЕФЙиЯЕ(ЮЛжУЙиЯЕМАЪ§СПЙиЯЕ)ЃЌЧыжБНгаДГіФуЕУЕНЕФНсТлЃЛ
ЃЈ2ЃЉНЋе§ЗНаЮDEFGШЦЕуDФцЪБеыЗНЯђа§зЊвЛНЧЖШІСКѓ(0ЁуЃМІСЃМ90Ёу)ЃЌШчЭМ(2)ЃЌЭЈЙ§ЙлВьЛђВтСПЕШЗНЗЈХаЖЯ(1)жаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШчЙћГЩСЂЃЌЧыгшвджЄУїЃЛШчЙћВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєBCЃНDEЃН2ЃЌе§ЗНаЮDEFGШЦЕуDФцЪБеыЗНЯђа§зЊНЧЖШІС (0ЁуЃМІСЃМ360Ёу)Й§ГЬжаЃЌЕБBGЮЊзюаЁжЕЪБЃЌЧѓAFЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯрЕШЧвДЙжБЃЛЃЈ2ЃЉГЩСЂЃЌМћНтЮіЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪКЭе§ЗНаЮЕФаджЪЕУГіDG=DEЃЌAD=BDЃЌНјЖјЕУГіЁїBDGЁеЁїADEЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉбгГЄEAЗжБ№НЛDGЁЂBGгкЕуNЁЂMСНЕуЃЌЪзЯШжЄУїЁїBDGЁеЁїADEЃЌНјЖјЕУГіBGЁЭAEЧвBG=AEЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌвЊЪЙAEзюДѓЃЌжЛвЊНЋе§ЗНаЮШЦЕуDФцЪБеыа§а§зЊ270ЁуЃЌМДAЃЌDЃЌEдквЛЬѕжБЯпЩЯЪБЃЌAEзюДѓЃЌНјЖјЧѓГіМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЈ1ЃЉ
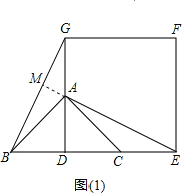
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=90ЁуЃЌЕуDЪЧBCЕФжаЕуЃЌ
ЁрBD=CD=ADЃЌ
ЁпдкЁїBDGКЭЁїADEжа
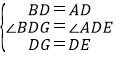
ЁрЁїBDGЁеЁїADEЃЈSASЃЉЃЌ
ЁрBG=AEЃЌЁЯDGB=ЁЯDEAЃЌ
бгГЄEAЕНBGгквЛЕуMЃЌ
ЁрЁЯGAM=ЁЯDAEЃЌ
ЁрЁЯGMA=ЁЯEDA=90ЁуЃЌ
ЁрЯпЖЮBGКЭAEЯрЕШЧвДЙжБЃЛ
ЃЈ2ЃЉГЩСЂЃЌ
ШчЭМЃЈ2ЃЉЃЌбгГЄEAЗжБ№НЛDGЁЂBGгкЕуMЁфЁЂNЁфСНЕуЃЌ
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=90ЁуЃЌЕуDЪЧBCЕФжаЕуЃЌ
ЁрЁЯADB=90ЁуЃЌЧвBD=ADЃЌ
ЁпЁЯBDG=ЁЯADB-ЁЯADG=90Ёу-ЁЯADG=ЁЯADEЃЌ
ЁпдкЁїBDGКЭЁїADEжа
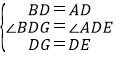
ЁрЁїBDGЁеЁїADEЃЈSASЃЉЃЌ
ЁрBG=AEЃЌЁЯDEA=ЁЯDGBЃЌ
ЁпЁЯDEA+ЁЯDNE=90ЁуЃЌЁЯDNE=ЁЯMNGЃЌ
ЁрЁЯMNG+ЁЯDGM=90ЁуЃЌ
МДBGЁЭAEЧвBG=AEЃЛ
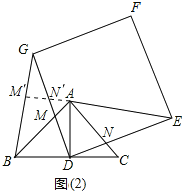
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌвЊЪЙAEзюДѓЃЌжЛвЊНЋе§ЗНаЮШЦЕуDФцЪБеыа§а§зЊ270ЁуЃЌМДAЃЌDЃЌEдквЛЬѕжБЯпЩЯЪБЃЌAEзюДѓЃЛ
Ёпе§ЗНаЮDEFGдкШЦЕуDа§зЊЕФЙ§ГЬжаЃЌEЕудЫЖЏЕФЭМаЮЪЧвдЕуDЮЊдВаФЃЌDEЮЊАыОЖЕФдВЃЌ
ЁрЕБе§ЗНаЮDEFGа§зЊЕНGЕуЮЛгкBCЕФбгГЄЯпЩЯЃЈМДе§ЗНаЮDEFGШЦЕуDФцЪБеыЗНЯђа§зЊ270ЁуЃЉЪБЃЌBGзюДѓЃЌШчЭМЃЈ3ЃЉЃЌ
ШєBC=DE=mЃЌдђAD=![]() ЃЌEF=mЃЌ
ЃЌEF=mЃЌ
дкRtЁїAEFжаЃЌAF2=AE2+EF2=ЃЈAD+DEЃЉ2+EF2=![]()
ЁрAF=![]() ЃЌМДдке§ЗНаЮDEFGа§зЊЙ§ГЬжаЃЌЕБAEЮЊзюДѓжЕЪБЃЌAF=
ЃЌМДдке§ЗНаЮDEFGа§зЊЙ§ГЬжаЃЌЕБAEЮЊзюДѓжЕЪБЃЌAF=![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИіЬхОгЊЛЇСЫНтЕНгавЛжжКазАЩЬЦЗФмГЉЯњЪаГЁЃЌОЭгУ4ЭђдЊЙКНјетжжЩЬЦЗЃЌУцЪаКѓЙћШЛЙЉВЛгІЧѓЃЌЫћгжгУ8.8ЭђдЊЙКНјСЫЕкЖўХњетжжЩЬЦЗЃЌЫљЙКЪ§СПЪЧЕквЛХњЙКНјСПЕФ2БЖЃЌЕЋУПКаЕЅМлеЧСЫ4дЊЃЌЫћдкЯњЪлетжжКазАЩЬЦЗЪБУПКаЖЈМлЖМЪЧ56дЊЃЌзюКѓЪЃЯТЕФ150КаАДАЫелЯњЪлЃЌКмПьЪлЭъЃЌдкетСНБЪЩњвтжаЃЌетЮЛИіЬхОгЊЛЇЙВгЎРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЁЯA=70ЁуЃЌНЋЦНааЫФБпаЮABCDШЦЕуBЫГЪБеыа§зЊЕНЦНааЫФБпаЮA1BC1D1ЕФЮЛжУЃЌДЫЪБC1D1ЧЁКУОЙ§ЕуCЃЌдђЁЯABA1=______ЁуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊA(Ѓ2ЃЌ1)ЃЌB(Ѓ1ЃЌ4)ЃЌC(Ѓ3ЃЌ2)ЃЎ
(1)ЛГіЁїABCЙигкЕуBГЩжааФЖдГЦЕФЭМаЮЁїA1BC1ЃЛ
(2)вддЕуOЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ1ЁУ2ЃЌдкyжсЕФзѓВрЃЌЛГіЁїABCЗХДѓКѓЕФЭМаЮЁїA2B2C2ЃЌВЂжБНгаДГіЕуC2ЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЧНБпгаСНИљФОИЫЃЎ
(1)ФГвЛЪБПЬМзФОИЫдкбєЙтЯТЕФгАзгШчЭМЫљЪОЃЌФуФмЛГіввФОИЫЕФгАзгТ№ЃП(гУЯпЖЮБэЪОгАзг)
(2)ЕБввФОИЫвЦЖЏЕНЪВУДЮЛжУЪБЃЌЦфгАзгИеКУВЛТфдкЧНЩЯЃП
(3)дкФуЫљЛЕФЭМжагаЯрЫЦШ§НЧаЮТ№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§yЃНЉx+mКЭyЃН2x+nЕФЭМЯѓЖМОЙ§AЃЈЉ4ЃЌ0ЃЉЃЌЧвгыyжсЗжБ№НЛгкBЁЂCСНЕуЃЌдђЁїABCЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.48B.36C.24D.18
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
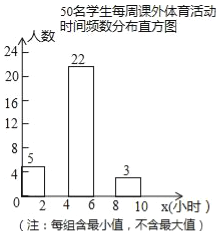
ЁОЬтФПЁПЮЊСЫСЫНтФГбЇаЃАЫФъМЖбЇЩњУПжмЦНОљЬхг§ЖЭСЖЪБМфЕФЧщПіЃЌЫцЛњГщВщСЫИУФъМЖЕФВПЗжбЇЩњЃЌЖдЦфУПжмЖЭСЖЪБМфНјааЭГМЦЃЌИљОнЭГМЦЪ§ОнЛцжЦГЩЭМ1КЭЭМ2СНИіВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
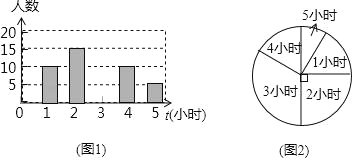
ЃЈ1ЃЉБОДЮЙВГщШЁСЫбЇЩњЁЁ ЁЁШЫЃЌВЂЧыНЋЭМ1ЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉетзщЪ§ОнЕФжаЮЛЪ§ЪЧЁЁ ЁЁЃЌЧѓГіетзщЪ§ОнЕФЦНОљЪ§ЃЛ
ЃЈ3ЃЉШєАЫФъМЖгабЇЩњ1800ШЫЃЌЧыФуЙРМЦЬхг§ЖЭСЖЪБМфЮЊ3аЁЪБЕФбЇЩњгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊдіЧПбЇЩњЬхжЪЃЌИїбЇаЃЦеБщПЊеЙСЫбєЙтЬхг§ЛюЖЏЃЌФГаЃЮЊСЫНтШЋаЃ1000УћбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфЕФЧщПіЃЌЫцЛњЕїВщСЫЦфжаЕФ50УћбЇЩњЃЌЖдет50УћбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфxЃЈЕЅЮЛЃКаЁЪБЃЉНјааСЫЭГМЦЃЎИљОнЫљЕУЪ§ОнЛцжЦСЫвЛЗљВЛЭъећЕФЭГМЦЭМЃЌВЂжЊЕРУПжмПЮЭтЬхг§ЛюЖЏЪБМфдк6ЁмxЃМ8аЁЪБЕФбЇЩњШЫЪ§еМ24%ЃЎИљОнвдЩЯаХЯЂМАЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщЪєгк ЕїВщЃЌбљБОШнСПЪЧ ЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМжаПеШБЕФВПЗжЃЛ
ЃЈ3ЃЉЧѓет50УћбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфЕФЦНОљЪ§ЃЛ
ЃЈ4ЃЉЙРМЦШЋаЃбЇЩњУПжмПЮЭтЬхг§ЛюЖЏЪБМфВЛЩйгк6аЁЪБЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
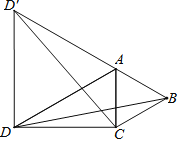
ЁОЬтФПЁПШчЭМЃЌдкЁїACDжаЃЌAD=9ЃЌCD=![]() ,ЁїABCжаЃЌAB=ACЃЌШєЁЯCAB=60Ёу,ЁЯADC=30Ёу,дкЁїACDЭтзїЕШБпЁїADDЁф
,ЁїABCжаЃЌAB=ACЃЌШєЁЯCAB=60Ёу,ЁЯADC=30Ёу,дкЁїACDЭтзїЕШБпЁїADDЁф
ЃЈ1ЃЉЧѓжЄЃКBD=CDЁф
ЃЈ2ЃЉЧѓBDЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com